Question 1168621: find the equation of the ellipse in general form with vertices at (-2,1) and (4,1) with eccentricity of ⅔
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website! find the equation of the ellipse in general form with vertices at ( , ) and ( ,) with eccentricity of 
the equation of the ellipse in general form:
The distance from the center to a vertex is the fixed value  .
 =>  ->  and 
then
so far equation is:
The distance from the center to a vertex is the fixed value .
Since the vertices of the ellipse are (,) and (,) , and then
( ,)=(,)
( ,)=(,)
=>  , 
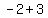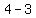and your equation is:
|
|
|
