Question 1168599: 8) Use the Rational Zero Theorem to list all possible rational zeros for the given function
f(x) = - 2x ^ 3 + 3x ^ 2 - 4x + 8
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the Rational Zero Theorem to list all possible rational zeros for the given function

Since all coefficients are integers, we can apply the rational zeros theorem.
The trailing coefficient (coefficient of the constant term) is  . .
Find its factors (with plus and minus): ± ,± ,± ,± ,± ,± ,± . These are the possible values for . These are the possible values for  . .
The leading coefficient (coefficient of the term with the highest degree) is  . .
Find its factors (with plus and minus): ± ,± ,± . These are the possible values for . These are the possible values for  . .
Find all possible values of  : :
± ,± ,± ,± ,±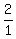 ,± ,±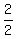 ,± ,± ,± ,± ,± ,± ,± ,±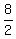 . .
Simplify and remove duplicates (if any), these are  rational roots: ± rational roots: ± ,± ,± ,± ,± ,± ,± ,± ,±
Next, check the possible roots:
if  is a is a  of the polynomial of the polynomial  , the remainder from the division of , the remainder from the division of  by by  should equal should equal  . .
Check  : divide : divide 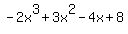 by by  .The quotient is .The quotient is 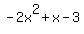 and the remainder is and the remainder is  (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 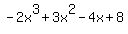 by by  .The quotient is .The quotient is 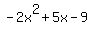 and the remainder is and the remainder is  (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 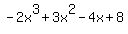 by by 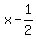 .The quotient is .The quotient is 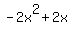 and the remainder is and the remainder is 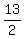 (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 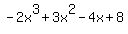 by by 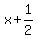 .The quotient is .The quotient is 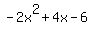 and the remainder is and the remainder is  (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 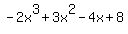 by by  .The quotient is .The quotient is 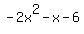 and the remainder is and the remainder is  (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 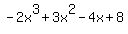 by by  .The quotient is .The quotient is  and the remainder is and the remainder is  (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 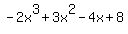 by by  .The quotient is .The quotient is 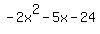 and the remainder is and the remainder is 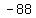 (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 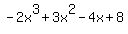 by by  .The quotient is .The quotient is 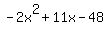 and the remainder is and the remainder is 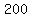 (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 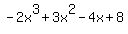 by by 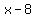 .The quotient is .The quotient is 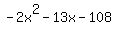 and the remainder is and the remainder is 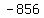 (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
Check  : divide : divide 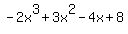 by by  .The quotient is .The quotient is  and the remainder is and the remainder is 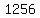 (use the synthetic division calculator to see the steps). (use the synthetic division calculator to see the steps).
so, none of these possible rational roots ± ,± ,± ,± ,± ,± ,± ,± ,± are real roots of given function because long division by them does not gives us reminder are real roots of given function because long division by them does not gives us reminder 
|
|
|