SOLUTION: Anna preston has $2.80 in nickels and quarters. She has twice as many nickels as quarters. How many of each kind of coin does she have?

Algebra ->  Equations -> SOLUTION: Anna preston has $2.80 in nickels and quarters. She has twice as many nickels as quarters. How many of each kind of coin does she have?      Log On


   

Question 1164993: Anna preston has $2.80 in nickels and quarters. She has twice as many nickels as quarters. How many of each kind of coin does she have?
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

Mental solution 

Group the coins in sets in a way each set contains two nickels and one quarter.


According to the condition, it is possible to do.


Then every set is worth 25+5+5 = 35 cents.


Having $2.80 = 280 cents, the number of such sets is 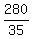 280%2F35 = 8.


Hence, the original collection has 8 quarters and 2*8 = 16 nickels.    ANSWER

Solved.


Algebra solution 

If n is the number of quarters, then the number of nickels is  (2n).


The total money equation is


    25n + 5*(2n) = 280  cents,   or

    25n + 10n = 280

    35n = 280

      n = 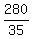280%2F35 = 8.


And you get the same answer.


The algebra solution follows the same logic as the mental solution above.


---------------

.
For coin problems and their detailed solutions see the lessons in this site:
    - Coin problems
    - More Coin problems
    - Solving coin problems without using equations
    - Kevin and Randy Muise have a jar containing coins
    - Typical coin problems from the archive
    - Three methods for solving standard (typical) coin word problems
    - More complicated coin problems
    - Advanced coin problems
    - Solving coin problems mentally by grouping without using equations
    - Non-typical coin problems
    - Santa Claus helps solving coin problem
    - OVERVIEW of lessons on coin word problems

You will find there the lessons for all levels - from introductory to advanced,
and for all methods used - from one equation to two equations and even without equations.

A convenient place to quickly observe these lessons from a  "bird flight height"  (a top view)  is the last lesson in the list.

Read them attentively and become an expert in this field.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Coin problems".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.