Question 1162695: I am needing help in setting up this equation:
A 96 ft rope is cut into 4 pieces. The second piece is 6 less than twice as long as the first piece. The third piece is 5 feet greater than the first piece. AndThe fourth is half as long as the second piece. How long is the fourth piece?
Found 5 solutions by ikleyn, VFBundy, solver91311, Theo, MathTherapy:
Answer by ikleyn(52785)   (Show Source):
You can put this solution on YOUR website! .
I am needing help in setting up this equation:
A 96 ft rope is cut into 4 pieces. The second piece is 6 less than twice as long as the first piece.
The third piece is 5 feet greater than the first piece. AndThe fourth is half as long as the second piece.
How long is the fourth piece?
~~~~~~~~~~~~~~~
Let x be the length of the first piece.
Then 2nd piece is (2x-6) ft.
3rd piece is (x+5) ft.
4th piece is 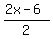 = x-3 ft.
Therefore, the equation for the total length is THIS
x + (2x-6) + (x+5) + (x-3) = 96 feet.
It is your setup.
Is everything clear to you in my post ?
Answer by VFBundy(438)  (Show Source):
You can put this solution on YOUR website! First piece = x
Second piece = 2x - 6
Third piece = x + 5
Fourth piece = (2x - 6)/2 = x - 3
(x) + (2x - 6) + (x + 5) + (x - 3) = 96
5x - 4 = 96
5x = 100
x = 20
The fourth piece is (x - 3) inches long. Plugging in x = 20, that comes out to 17 inches.
Answer by solver91311(24713)  (Show Source):
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! let the length of each piece be a, b, c, d.
you get:
a + b + c + d = 96
you get the following additional equations based on the problem statement.
b = 2a - 6
c = a + 5
d = b/2
the trick is to reduce the number of variables to 1.
then the problem can be solved.
we'll try to make everything in terms of a.
d = b/2 is not in terms of a, but we know that b = 2a - 6
replace b in the equation of d = b/2 to get d = (2a - 6) / 2
now you have everything in terms of a.
you have:
b = 2a - 6
c = a + 5
d = (2a - 6) / 2
a + b + c + d = 96 becomes:
a + (2a - 6) + (a + 5) + (2a - 6) / 2 = 96
simplify to get:
a + 2a - 6 + a + 5 + 2a/2 - 6/2 = 96
simplify further to get:
a + 2a - 6 + a + 5 + a - 3 = 96
combine like terms to get:
5a - 4 = 96
add 4 to both sides of the equation to get:
5a = 100
solve for a to get:
a = 100 / 5 = 20
b = 2a - 6 = 40 - 6 = 34
c = a + 5 = 25
d = b / 2 = 17
a + b + c + d = 20 + 34 + 25 + 17 = 96
solution is confirmed to be good.
solution is the fourth piece (piece d) is 17 feet in length.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
I am needing help in setting up this equation:
A 96 ft rope is cut into 4 pieces. The second piece is 6 less than twice as long as the first piece. The third piece is 5 feet greater than the first piece. AndThe fourth is half as long as the second piece. How long is the fourth piece?
Let the first piece's length be F
Then lengths of the 2nd, 3rd, and 4th pieces are: 2F - 6, F + 5, and  , respectively
Since all pieces' lengths sum to 96 ft, we get: F + 2F - 6 + F + 5 + F - 3 = 96
This should be a pretty straight-forward equation at this time! Just combine like-terms and solve, from here.
Are some of these people ADDICTED to solving, or do they just not care to practice what they're supposed to be preaching: READING THE PROBLEM before responding. Didn't the person ask for the SETUP?
Did 2 of them SEE that? The problem asks for the length of the 4th piece but the person who asked for help just wants help to set it up!!
|
|
|
