Question 1160899: In solving this equation, (x-3)/(x+2)=(x+2)/(x-3) you could cross multiply and get (x-3)^2=(x+2)^2 but you can't simply take the square root of each side because then you get x-3=x+2 and hence 0=5 which is wrong. If you multiply (x-3)(x-3) and (x+2)(x+2) and get x^2-6x+9=x^2+4x+4 then it is solved, x=1/2. My question is, WHY can't you take the square root of both sides, as mentioned earlier? Thank you so much for your help.
Found 3 solutions by Boreal, MathTherapy, ikleyn:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! sqrt(x-3)^2=+/- (x-3)
sqrt(x+2)^2=+/- (x+2)
But the original fractions are not defined when x=-2 or x=3
So when you cross-multiply, you get (x-3)^2, but it is not defined at x=3.
One has to go back to the original function and look at the domain.
Remember in completing the square problems, one has +/- results
you can get to x=1/2 if (x-3)=-(x+2)=-x-2
then 2x=1 and x=1/2, but that is allowing, if one will, an x-3 from one side, where 3 is in the domain, and x=-2 from the other side, where -2 is part of the domain, if one will, for the numerator.
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website! In solving this equation, (x-3)/(x+2)=(x+2)/(x-3) you could cross multiply and get (x-3)^2=(x+2)^2 but you can't simply take the square root of each side because then you get x-3=x+2 and hence 0=5 which is wrong. If you multiply (x-3)(x-3) and (x+2)(x+2) and get x^2-6x+9=x^2+4x+4 then it is solved, x=1/2. My question is, WHY can't you take the square root of both sides, as mentioned earlier? Thank you so much for your help.
 ----- Cross-multiplying
A lot of people FORGET, I believe, that when taking the square root of an expression, it's IMPERATIVE to indicate that the resulting expression can either be - (negative), or + (positive).
Taking the square root of both sides, we get: 
 
OR
Taking the square root of both sides, we get: 
 
Another VERY IMPORTANT fact is that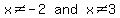 
Answer by ikleyn(52776)  (Show Source):
|
|
|
