SOLUTION: Hello I need an explanation on this problem, not a solve. Kira drove 200 miles from San Diego to Santa Barbara. On the return trip, she decreased her speed by 10 mph, and the

Click here to see ALL problems on Equations

Question 1160712: Hello
I need an explanation on this problem, not a solve.
Kira drove 200 miles from San Diego to Santa Barbara. On the return trip, she decreased her speed by 10 mph, and the trip took an extra hour. What was her speed on the way back?
Going: 200/x
Return: 200/x-10
200/x + 1 = Return: 200/x-10
I’m confused as to why we add one to going and not on return since that statement comes after she decreased her speed.
Thanks in advance.
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website!
.

Let x be her speed driving to Santa Barbara, in miles per hour. Then her speed driving back is (x-10) mph, according to the condition. The time driving "to there" is hours (the distance divided by speed). The time driving back is hours. Time back is one hour longer than the time "to there". It gives you THIS EQUATION - = 1 hour. It is the major step of the solution to establish this equation. It is called "time" equation, since each its term is the time. From this point, I just see / guess the solution mentally: x = 50 miles per hour. To solve the equation formally, multiply both sides by x*(x-10). You will get 200x - 200*(x-10) = x*(x-10). Simplify and solve for x 2000 = x^2 - 10x, x^2 - 10x - 1000 = 0. Factor left side (x-50)*(x+40) = 0. The solution is x= 50 mph (exactly as I guessed above). CHECK. Time to Santa Barbara is = 4 hours. Time driving back is = = 5 hourrs. The difference is 5 hours - 4 hours = 1 hour. ! Precisely correct !

------------

The problem is just solved, explained and completed.

I hope everything is clear to you.

In any case, you will not get better explanation NOWHERE.

Do not forget to post your "THANKS" to me for my solution/lesson.

Answer by MathTherapy(10552) (Show Source):
You can put this solution on YOUR website!
Hello
I need an explanation on this problem, not a solve.
Kira drove 200 miles from San Diego to Santa Barbara. On the return trip, she decreased her speed by 10 mph, and the trip took an extra hour. What was her speed on the way back?
Going: 200/x
Return: 200/x-10
200/x + 1 = Return: 200/x-10
I’m confused as to why we add one to going and not on return since that statement comes after she decreased her speed.
Thanks in advance.

Obviously, a TIME equation is used here, to solve.
As observed the OUTBOUND speed is named, x
Since the RETURN speed was 10 mph LESS, then return speed = x - 10
With both distances being the same (200 miles), TIME taken to get to destination was: , and TIME taken to return was: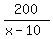
Since the RETURN time was an EXTRA hour, this also means that the time to get there was 1 hour LESS than the time taken to return. Therefore, we need to
ADD 1 hour to the time it took to get to the destination, to get the time it took to make the RETURN TRIP, especially since the speed was reduced.
Now, we apply the TIME equation above to get: , which becomes:
Do you now understand this?