Question 1158664: a ball is dropped from a height of 2 meters and bounces up to 3/4 of its previous height on each bounce. using geometric series, how much TOTAL DISTANCE (up and down) does the ball travel until it stops bouncing?
Found 2 solutions by Shin123, ikleyn:
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! The ball keeps bouncing a fraction of its height. The ball in theory never stops bouncing (but in real life, it eventually does). So it is an infinite geometric sequence.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this problem, the sequence is close to be a Geometric progression, but actually, is not.
It requires an ACCURATE analysis. First time the ball falls down; then every next bouncing, it goes UP and DOWN
The total distance is the sum of these values
Down Up and Up and Up and Up and
down down down down
2 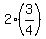 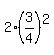 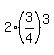 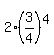 Coefficient 1 2 2 2 2 <<<---=== this coefficient accounts for "up and down"
So the total distance is
2 + 2*S, where S is the infinite geometric progression with the first term a =
Coefficient 1 2 2 2 2 <<<---=== this coefficient accounts for "up and down"
So the total distance is
2 + 2*S, where S is the infinite geometric progression with the first term a = 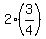 = =  and the common ratio r = and the common ratio r =  .
The sum of this infinite progression is S = .
The sum of this infinite progression is S =  = = 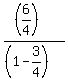 = = 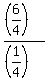 = 6.
Therefore, the ANSWER to the problem question is 2 + 2*6 = 14 meters. = 6.
Therefore, the ANSWER to the problem question is 2 + 2*6 = 14 meters.
Solved.
-------------
So, this problem has a "trap".
Those who have experience in solving/teaching/explaining such problems, know about it.
All the others, as a rule, go directly to this trap.
|
|
|