Question 1153986: The table lists a readings for three years.
(a) If the quadratic relationship between the carbon dioxide concentration C and the year t is expressed as Upper C equals at squared plus bt plus c, where t equals 0 corresponds to 1962, use a system of linear equations to determine the constants a, b, and c, and give the equation.
(b) Predict the year when the amount of carbon dioxide in the atmosphere will double from its 1962 level.
Year.
1962
1982
2002
CO2
319
340
368
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! The table lists a readings for three years.
(a) If the quadratic relationship between the carbon dioxide concentration  and the year and the year  is expressed as is expressed as  , where , where  equals equals  corresponds to 1962, use a system of linear equations to determine the constants corresponds to 1962, use a system of linear equations to determine the constants  , ,  , and , and  , and give the equation. , and give the equation.
Year.
1962
1982
2002
CO2
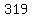



since  equals equals  corresponds to 1962, and corresponds to 1962, and  is is 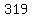


 ................year 1982, ................year 1982,  , ,  , , 


 .......solve for .......solve for 
 .................eq.1 .................eq.1
 ................year 2002, ................year 2002,  , ,  , , 




 ........eq.2 ........eq.2
from eq.1 and eq.2 we have




go to
 .................eq.1, plug in .................eq.1, plug in


your equation is:

(b) Predict the year when the amount of carbon dioxide in the atmosphere will double from its 1962 level.
1962 level is 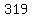
in  years will double which is years will double which is 
 .........sole for .........sole for 


using quadratic formula, we get
 => exact solution (only positive root, we will disregard negative solution) => exact solution (only positive root, we will disregard negative solution)
 -> approximately -> approximately
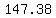 years from 1962 is: year years from 1962 is: year 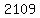 and the amount of carbon dioxide in the atmosphere will double from its 1962 level. and the amount of carbon dioxide in the atmosphere will double from its 1962 level.
check:




Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|