.
 +
+ 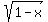 +
+ 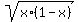 = 1. (1)
The domain, where all included functions are defined, is the segment [0,1].
Two obvious solutions to the given equation in this domain are x= 0 and x= 1.
Below I will show that the given equation HAS NO other solutions.
Indeed, let 0 < x < 1.
Then
= 1. (1)
The domain, where all included functions are defined, is the segment [0,1].
Two obvious solutions to the given equation in this domain are x= 0 and x= 1.
Below I will show that the given equation HAS NO other solutions.
Indeed, let 0 < x < 1.
Then  is defined and is positive number
is defined and is positive number  > 0.
Similarly,
> 0.
Similarly, 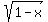 is defined and is positive number
is defined and is positive number 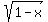 > 0.
For any two real positive numbers "a" and "b" the following inequality is valid
a + b >
> 0.
For any two real positive numbers "a" and "b" the following inequality is valid
a + b > 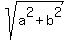 . (2)
To prove it, square both sides. You will get
a^2 + 2ab + b^2 > a^2 + b^2,
which is valid for all positive "a" and "b".
Now apply the inequality (2) for a=
. (2)
To prove it, square both sides. You will get
a^2 + 2ab + b^2 > a^2 + b^2,
which is valid for all positive "a" and "b".
Now apply the inequality (2) for a=  and b=
and b= 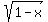 . You will get
. You will get
 +
+ 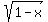 >
> 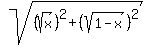 =
= 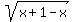 =
= 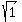 = 1.
Thus, the sum
= 1.
Thus, the sum  +
+ 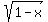 at 0 < x < 1 is just greater than 1.
With the added positive addend
at 0 < x < 1 is just greater than 1.
With the added positive addend 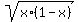 , the sum
, the sum  +
+ 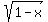 +
+ 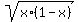 is just even more than 1.
Therefore, the sum
is just even more than 1.
Therefore, the sum  +
+ 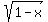 +
+ 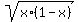 can not be equal to 1 at 0 < x < 1.
Thus, it is PROVED that the given equation has no solutions inside the segment [0,1].
So, the endpoints x= 0 and x= 1 are the only solutions.
can not be equal to 1 at 0 < x < 1.
Thus, it is PROVED that the given equation has no solutions inside the segment [0,1].
So, the endpoints x= 0 and x= 1 are the only solutions.
-------------
Solved.