Question 1152365: √(10-x)+√(3+x)+2√(30+7x-x^2)=17
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution can be done in much simpler way.
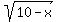 + + 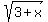 + + 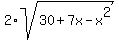 = 17 (1) = 17 (1)
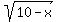 + + 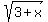 = 17 - = 17 - 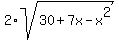 Square both sides
(10-x) +
Square both sides
(10-x) + 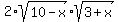 + (3+x) = 17 - + (3+x) = 17 - 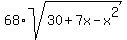 + 4*(30 +7x - x^2)
Notice that (10-x)*(3+x) = 30 + 7x - x^2, and continue transform preceding equations
(10-x) + + 4*(30 +7x - x^2)
Notice that (10-x)*(3+x) = 30 + 7x - x^2, and continue transform preceding equations
(10-x) + 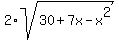 + (3+x) = 289 - + (3+x) = 289 - 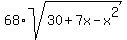 + 4*(30 +7x - x^2)
13 + + 4*(30 +7x - x^2)
13 + 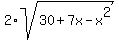 = 289 - = 289 - 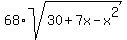 + 4*(30+7x-x^2)
0 = 276 - + 4*(30+7x-x^2)
0 = 276 - 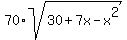 + 4*(30+7x-x^2) (2)
Introduce new variable t = + 4*(30+7x-x^2) (2)
Introduce new variable t = 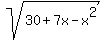 .
Then equation (2) takes the form
4t^2 - 70t + 276 = 0.
Solve it using the quadratic formula .
Then equation (2) takes the form
4t^2 - 70t + 276 = 0.
Solve it using the quadratic formula
 = = 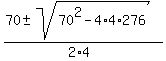 = = 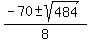 = = 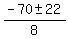 .
Case 1. t = .
Case 1. t = 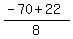 = -6.
Then t = = -6.
Then t = 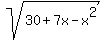 = -6 implies (after squaring both sides)
30 + 7x - x^2 = 36
x^2 - 7x + 6 = 0
(x-1)*(x-6) = 0
The roots are x= 1 and x= 6.
You can easily check that both these roots satisfy the original equation.
Case 2. t = = -6 implies (after squaring both sides)
30 + 7x - x^2 = 36
x^2 - 7x + 6 = 0
(x-1)*(x-6) = 0
The roots are x= 1 and x= 6.
You can easily check that both these roots satisfy the original equation.
Case 2. t = 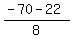 = -11.5.
Then t = = -11.5.
Then t = 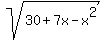 = -11.5 implies (after squaring both sides)
30 + 7x - x^2 = 132.25
x^2 - 7x + 102.25 = 0
Discriminant d = b^2 - 4ac = 7^2 - 4*102.25 is negative,
Hence, this case does not produce real solutions.
The solution is completed.
The ANSWER is: the original equation has two solutions x= 1 and x= 6. = -11.5 implies (after squaring both sides)
30 + 7x - x^2 = 132.25
x^2 - 7x + 102.25 = 0
Discriminant d = b^2 - 4ac = 7^2 - 4*102.25 is negative,
Hence, this case does not produce real solutions.
The solution is completed.
The ANSWER is: the original equation has two solutions x= 1 and x= 6.
Solved.
----------------
In her solution, tutor @MathLover1 makes a HUGE amount unnecessary work.
Also, on the way, she applies (without acknowledgement) Internet software to factor polynomials of high degrees (up to 8-th degree).
It is IMPOSSIBLE to get such factoring "by hands", without using software tools.
Obviously, this way is not accessible for real school Math student, and it is NOT the WAY to solve such problem for educational purposes.
The way which I propose in my post, is a real way, and, actually, the only real, accessible and right way to solve this problem.
|
|
|