Question 1150654: An object is projected directly upward from an initial height of 24 feet at an initial velocity of 96 feet per second. Write a model for the height of the object, s(t), after t seconds. Use s(t) = -16t^2+v+s.After how many seconds does the object reach its maximum height? What is the maximum height? After how many seconds does the object land on the ground?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! An object is projected directly upward from an initial height of 24 feet at an initial velocity of 96 feet per second.
Write a model for the height of the object, s(t), after t seconds.
Use s(t) = -16t^2+v+s.
v=96, s=24, therefore
s(t) = -16t^2 + 96t + 4
:
After how many seconds does the object reach its maximum height?
Max occurs at the axis of symmetry, (x = -b/2a),
in this equation a=-16, b=96 therefore
t = 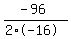
t = +3 sec for max height
:
What is the maximum height?
s(t) = the height, t=3 therefore
s)t) = -16(3^2) + 96(3) + 24
s(t) = -144 + 288 + 24
s(t) = 168 ft is the max height
:
After how many seconds does the object land on the ground?
then the height = 0, therfore
-16t^2 + 96t + 24 = 0
simplify divide by -4
4t - 24t - 6 = 0
Use the quadratic formula, a=4, b=-24, c=-6
the positive solution is
t ~ 6.24 seconds to reach the ground
|
|
|