.
First divide both sides by 9. You will get an EQUIVALENT equation
cos(2theta) = - cos(theta)
Next, use the standard basic trigonometry formula
cos(2theta) = 2*cos^2(theta) - 1.
Then equation (1) takes the form
cos^2(theta) = -cos(theta), or
cos^2(theta) + cos(theta) = 0.
Factor it
cos(theta)*(cos(theta) + 1) = 0.
Hence, EITHER cos(theta) = 0, giving solutions  =
= 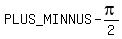 +
+  , k = 0, +-1, +-2, . . .
OR cos(theta) = -1, giving solutions
, k = 0, +-1, +-2, . . .
OR cos(theta) = -1, giving solutions  =
= 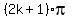 , k = 0, +-1, +-2, . . .
, k = 0, +-1, +-2, . . .
Completed, solved and explained in all details, with steps.