Question 1143268: The sum of two whole number is 45. Their difference is less than 10.the number of all possible pair is
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
0 is considered a whole number.
 Solve the first for y. y = 45-x.
Substitute in the inequality:
Solve the first for y. y = 45-x.
Substitute in the inequality:
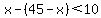
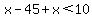
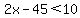
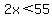
 x can be 0,1,2,...27
Solve the first for x. x = 45-y.
Substitute in the inequality:
x can be 0,1,2,...27
Solve the first for x. x = 45-y.
Substitute in the inequality:
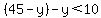
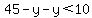
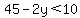
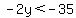
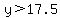 <--- we flip the inequality sign when we divide by a negative!
y can be any of 45,44,43, ..., 19,18
There are 28 whole numbers that x can be
So x can be any of 0, 1, 2, ..., 26,27
and y can be any of 45,44,43, ..., 19,18
(0,45), (1,44), (2,43), (3,42), (4,41),
(5,40), (6,39), (7,38), (8,37), (9,36),
(10,35), (11,34), (12,33), (13,32), (14,31),
(15,30), (16,29), (17,28), (18,27), (19,26),
(20,25), (21,24), (22,23), (23,22), (24,21),
(25,20), (26,19), (27,18)
Notice that the difference can be a negative number,
and that is the case is all but the last five in the list.
Edwin <--- we flip the inequality sign when we divide by a negative!
y can be any of 45,44,43, ..., 19,18
There are 28 whole numbers that x can be
So x can be any of 0, 1, 2, ..., 26,27
and y can be any of 45,44,43, ..., 19,18
(0,45), (1,44), (2,43), (3,42), (4,41),
(5,40), (6,39), (7,38), (8,37), (9,36),
(10,35), (11,34), (12,33), (13,32), (14,31),
(15,30), (16,29), (17,28), (18,27), (19,26),
(20,25), (21,24), (22,23), (23,22), (24,21),
(25,20), (26,19), (27,18)
Notice that the difference can be a negative number,
and that is the case is all but the last five in the list.
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The analysis and the answer by Edwin are incorect: he gives many "solutions", that are not the solutions at all.
I came to fix it.
Let x is the greatest of the two numbers x and y satisfying the condition.
Then
x + y = 45, (1)
x - y < 10. (2)
Express y = 45 - x from (1) and substitute it into (2). You will get
x - (45-x) < 10.
2x - 45 < 10
2x < 10 + 45 = 55
x < 55/2 = 27.5.
So, the solutions are these 5 pairs (x,y), where y = 45-x, x is the largest of the two numbers and x-y < 10 :
(27,18), (26, 19), (25,20), (24,21), (23,22). (*)
Five reversed pairs
(18,27), (19,26), (20,25), (24,21), (22,23) (**)
are the solutions to the original problem, too.
So, 10 pairs (*) and (**), and only they, are the solutions to the problem.
ANSWER. The number of all possible pairs is 10.
|
|
|