Question 1142063: The end of the seventh month this year, you have $503 saved. At the end of the tenth month this year, you have saved $545.
Write an equation to model this situation (use
m
for months and
s
for savings).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! at the end of the 7th month, you have 503.
at the end of the 10th month, you have 545.
if you look at this as a straight line equation, the equqtion for that is y = mx + b.
m is the slope and b is the y-intercept.
your slope is the change in y divided by the corresponding change in x.
your change in y would be (545 - 503) = 42
your corresponding change in x would be (10 - 7) = 3
your slope is 42 / 3 = 14.
your equation becomes y = 14 * x + b
your y-intercept is the value of y when x = 0.
to find that, you take any point on the line and replace x and y with that and solve for b.
one point on your line will be (7,503).
7 is equal to x and 503 is equal to y.
y = 14 * x + b becomes 503 = 14 * 7 + b
solve for b to get b = 503 - 14 * 7 = 503 - 98 = 405
your equation becomes y = 14 * x + 405
your y-intercept is 405.
this is the value of y when x is equal to 0.
when x is 7, you get y = 14 * x + 405 becomes y = 14 * 7 + 405 which becomes y = 98 + 405 which becomes y = 503.
when x is 10, you get y = 14 * x + 405 becomes y = 14 * 10 + 405 which becomes y = 140 + 405 which becomes y = 545.
that equation can be graphed.
the graph looks like this.
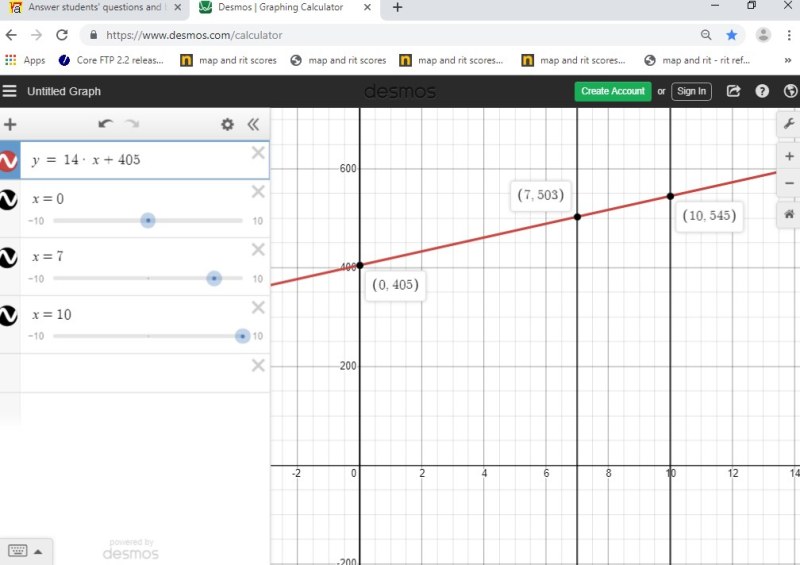
the above equation assumes straight line growth.
for each increase of 1 unit in the value of x, the value of y is increased by 14 units.
when dealing with x and y, the equation is y = 14 * x + 405.
if you replace y with s (savings), and x with m (for months), the equation becomes:
s = 14 * m + 405.
that tells you that, for every increase of 1 in the number of months, the value of your savings is increased by an average of 14.
|
|
|