Question 1136850: Find the standard form of the equation of the ellipse with the given characteristics. Center: (6, 7); a = 3c; foci: (2, 7), (10, 7)
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
c is the distance from the center of the ellipse to each focus. The coordinates of the center and the two foci tell us c=4; that makes a, the semi-major axis, 3c = 12.
a, b, and c in an ellipse are related by c^2 = a^2-b^2; that gives us b, the semi-minor axis, equal to 8*sqrt(2).
The standard form of the equation of an ellipse with center (h,k), semi-major axis a, and semi-minor axis b is

You have all the numbers to fill in to write the equation.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the standard form of the equation of the ellipse with the given characteristics.
Center: ( , ,  ); );
 ; ;
foci: ( , ,  ), ( ), ( , ,  ) )
The equation of an ellipse is :
 for a horizontally oriented ellipse and for a horizontally oriented ellipse and
 for a vertically oriented ellipse. for a vertically oriented ellipse.
( , , ) is the center and the distance ) is the center and the distance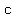 from the center to the foci is given by from the center to the foci is given by 
 is the distance from the center to the vertices and is the distance from the center to the vertices and 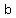 is the distance from the center to the co-vertices. is the distance from the center to the co-vertices.
The center of the ellipse is ( , ,  )=> )=> and and 
 is the distance between the center and the vertices, so is the distance between the center and the vertices, so 
 is the distance between the center and the foci, and foci is at ( is the distance between the center and the foci, and foci is at ( , ,  ), ( ), ( , ,  ) )
distance from  to to  is is  , and distance from , and distance from  to to  is is 
so 
since  , we have , we have  => =>
now find 




 for a horizontally oriented ellipse for a horizontally oriented ellipse

|
|
|