Question 1136257: NASA launches a rocker at T=0 seconds. It's height, in meters above sea level, as a function of time is given by H(T)=-4.9T^2 + 229T +185.
Assuming that the rocket will splash down into the ocean, at what time does splashdown occur?
The rocket splashes down after ___ seconds
How high above sea-level does the rocket get at its peak?
The rocket peaks at ___ meters above sea-level
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! ASA launches a rocker at T=0 seconds. It's height, in meters above sea level, as a function of time is given by H(T)=-4.9T^2 + 229T +185.
Assuming that the rocket will splash down into the ocean, at what time does splashdown occur?
=================
it's = it is.
---------
I would solve the problem, but these entries irritate me.
===================================
The rocket splashes down after ___ seconds
---
How high above sea-level does the rocket get at its peak?
---
The rocket peaks at ___ meters above sea-level
===============
this is not useful.
************************************************
H(T)=-4.9T^2 + 229T +185
At impact, h(t) = 0
-4.9T^2 + 229T +185 = 0
Solve for t
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=56067 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 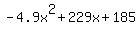 can be factored: can be factored:

Again, the answer is: -0.794358402485433, 47.5290522800364.
Here's your graph:
 |
Ignore the negative value.
t = ~ 47.529 seconds
*************************************************
The peak (max height) is the vertex of the parabola, at t = -b/2a
t = -229/-9.8 = ~ 23.367 seconds
h(23.367) =~ 2675.5 meters
*************************************************
PS - this is not a rocket, it's a projectile.
Rockets accelerate upward.
|
|
|