Question 1132110: 2/x+5/y=5/6; x/2+y/5=5
Found 3 solutions by ikleyn, MathLover1, MathTherapy:
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
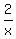 + + 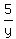 = =  , (1)
x/2 + y/5 = 5. (2)
This system of equations in non-linear.
To make the solution easier, I will introduce NEW VARIABLES a = , (1)
x/2 + y/5 = 5. (2)
This system of equations in non-linear.
To make the solution easier, I will introduce NEW VARIABLES a = 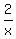 , b = , b = 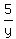 . Then the system takes the form
a + b = . Then the system takes the form
a + b =  (3) (3)
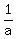 + +  = 5 (4)
To solve it, first simplify equation (4): = 5 (4)
To solve it, first simplify equation (4):
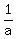 + +  = 5 ====> = 5 ====> 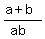 = 5 ====> replace a+b by = 5 ====> replace a+b by  , based on (3) ====> , based on (3) ====> 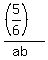 = 5 ====> ab = = 5 ====> ab =  .
Next, from (3), express b = .
Next, from (3), express b =  - a and substitute it into equation ab = - a and substitute it into equation ab =  . You will get . You will get
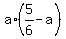 = =  ,
-6a^2 + 5a = 1
6a^2 - 5a + 1 = 0.
Solve the last quadratic equation using the quadratic formula.
You will get two solutions: a= ,
-6a^2 + 5a = 1
6a^2 - 5a + 1 = 0.
Solve the last quadratic equation using the quadratic formula.
You will get two solutions: a=  and a= and a=  .
Thus, the system (3)-(4) has two solutions:
1) a= .
Thus, the system (3)-(4) has two solutions:
1) a=  , b= , b=  - -  = = 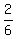 = =  ,
and
2) a = ,
and
2) a =  , b= , b=  - -  = =  = =  = =  .
Now you need to return from "a" and "b" to x and y, via the formulas a = .
Now you need to return from "a" and "b" to x and y, via the formulas a = 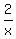 , b = , b = 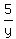 .
By doing so, you get two solutions for the original system:
1) x = .
By doing so, you get two solutions for the original system:
1) x = 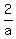 = = 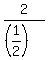 = 4; y = = 4; y = 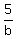 = = 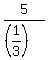 = 15.
2) x = = 15.
2) x = 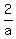 = = 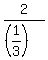 = 6; y = = 6; y = 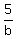 = = 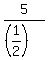 = 10.
Answer. The system has two solutions 1) x= 4; y= 15 and 2) x= 6, y= 10. = 10.
Answer. The system has two solutions 1) x= 4; y= 15 and 2) x= 6, y= 10.
Solved.
You may check that the solution is correct by substituting the found values into the original equations.
----------------
I am very glad that the tutor @MathLover1 placed her solution here.
Comparing these two, you can see how many tons of calculations I saved you from, using my substitutions ! ! !
==============
To see other similar solved problems for systems of two non-linear equations in two unknowns, look into the lessons
- Solving systems of non-linear equations by reducing to linear ones
- Solving systems of non-linear equations in two unknowns using the Cramer's rule
in this site.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by MathTherapy(10551)   (Show Source): (Show Source):
|
|
|