Question 1132097: How many ordered pairs of positive integers (x,y) satisfy the equation x=(4-x)/(y^2-x)?
My work: I am pretty sure that the only possible pair is (1,2), but I don’t know how to mathematically explain it... I just need help on this process.
Found 3 solutions by MathLover1, rothauserc, ikleyn:
Answer by MathLover1(20849)   (Show Source):
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! 1) x = (4-x)/(y^2-x)
:
xy^2 -x^2 = x^2 -x +4
:
xy^2 = x^2 -x +4
:
y^2 = (x^2 -x +4)/x
:
y = ((x^2 -x +4)/x)^(1/2)
:
here is a graph of the equation
:
:
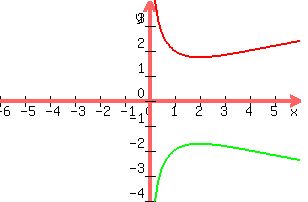
There are two integer solutions to equation 1, namely (1,2) and (1, -2) but the problem requires both coordinates (x, y) to be positive, therefore (1, -2) is rejected
:
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
The tutor @rothauserc was in one step from the final answer.
I came to make this last step and to complete the solution.
x = (4-x)/(y^2-x) (1)
x*(y^2-x) = 4 - x
xy^2 -x^2 = 4 - x
xy^2 = x^2 - x + 4
y^2 = (x^2 -x +4)/x
y =  =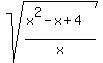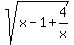 
Now look into the last formula.
The number 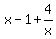 under the square root operator is integer only when
x=1 and x= 2 and x= 4.
For x larger than 4 we have the fraction under the square root, which CAN NOT give an integer number after taking the square root.
x= 1 gives y= +/-2.
x= 2 gives y= +/- , which is not integer.
x= 4 gives y= +/-2. But it makes the denominator of the equation (1) equal to zero, so it is ERRONEOUS solution.
ANSWER. The only solutions in integer numbers to equation (1) are these two pairs (x,y) = (1,2) and (x,y) = (1,-2).
Of them, only the pair (x,y) = (1,2) is the solution in positive integer numbers.
Solved.
|
|
|
