Question 1129304: A jet can travel 1000 miles against the wind in 2.5 hours. Going with the wind, the jet could travel 1250 miles in the same amount of time. Find the speed of the jet in still air and speed of the wind.
Found 4 solutions by ikleyn, josmiceli, Alan3354, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Against the wind the effective speed ("the ground speed") is
u - v = 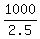 = 400 miles per hour. (1) (u = the speed of the jet in still air; v = the speed of the wind)
With the wind, the effective speed is
u + v = = 400 miles per hour. (1) (u = the speed of the jet in still air; v = the speed of the wind)
With the wind, the effective speed is
u + v = 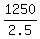 = 500 miles per hour. (2)
Add the equations (1) and (2)
2u = 400 + 500 = 900 ====> u = 900/2 = 450 mph is the speed of the jet in still air. ANSWER
Subtract eq(1) from eq(2)
2v = 100 ====> v = 50 mph is the speed of the wind. ANSWER = 500 miles per hour. (2)
Add the equations (1) and (2)
2u = 400 + 500 = 900 ====> u = 900/2 = 450 mph is the speed of the jet in still air. ANSWER
Subtract eq(1) from eq(2)
2v = 100 ====> v = 50 mph is the speed of the wind. ANSWER
Solved.
The lesson to learn from this solution and the tnings to memorize are :
1. The effective speed of a plane flying with a wind is the sum of the two speeds.
2. The effective speed of a plane flying against a wind is the difference of the two speeds.
3. It gives a system of two equations in two unknowns, which fits very well for solving by the elimination method.
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Once you find that the speed with the wind 1250/2.5 = 500mph and the speed against the wind is 1000/2.5=400mph, here is a simple and fast way to get the speeds of the plane and the wind without formal algebra.
The speed with the wind is the plane's speed plus the speed of the wind; the speed against the wind is the plane's speed minus the speed of the wind.
So the two numbers 500 and 400 are found, respectively, by starting with a first number and adding a second number, and by starting with the same first number and subtracting the second number.
If you visualize those operations on a number line, you can see that the first number has to be halfway between 500 and 400; then the second number has to be the difference between that first number and either 500 or 400.
Without all the words of explanation, the solution goes like this:
(1) the first number is halfway between 500 and 400: it is 450
(2) the second number is the difference between 450 and 500 (or between 450 and 400), which is 50.
This common sense solution can be used to quickly solve many similar problems. In its undisguised form, it might look like this:
The sum of two numbers is 30, their difference is 6. What are the two numbers?
Simple! The first number is halfway between 30 and 6: (30+6)/2 = 18. The second number is 30-18 = 12 (or 18-6 = 12).
|
|
|