SOLUTION: If the slant height of a cone is 4 times its radius, find the angle of the sector used to make the cone.

Algebra ->  Equations -> SOLUTION: If the slant height of a cone is 4 times its radius, find the angle of the sector used to make the cone.      Log On


   

Question 1129272: If the slant height of a cone is 4 times its radius, find the angle of the sector used to make the cone.
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

From the condition, the slant height  R is 4 times the cone radius  r :

    R = 4r.              (1)


If alpha is the angle under the question, then the length of the arc of the sector is

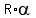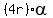    s = R%2Aalpha = %284r%29%2Aalpha.    (2)

   
At the same time, this length "s" is the circumference of the base of the cone:

    s = 2%2Api%2Ar.           (3)


Equating (2) and (3), you get

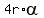    4r%2Aalpha = 2%2Api%2Ar.


Canceling "r" in both sides, you get

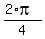    alpha = %282%2Api%29%2F4 = pi%2F2.       ANSWER


Answer.  The angle under the question is  pi%2F2.

Solved.