.
The equation
2x^2 - 2kx + 4 = 0
is equivalent to (after dividing both sides by 2)
x^2 - kx + 2 = 0. (1)
We are given that  is the root of the original equation; hence, the equation (1) with the leading coefficient 1 has this root, too.
Then, applying the Vieta's theorem, the other root of the equation (1) is
is the root of the original equation; hence, the equation (1) with the leading coefficient 1 has this root, too.
Then, applying the Vieta's theorem, the other root of the equation (1) is
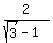 =
= 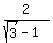 .
.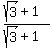 =
= 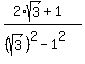 =
= 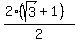 =
= 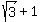 .
Thus we know BOTH ROOTS of the equation (1) (even without solving it explicitly (!) ). They are
.
Thus we know BOTH ROOTS of the equation (1) (even without solving it explicitly (!) ). They are
 and
and 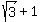 .
Again, according to Vieta's theorem, the sum of these roots is the coefficient at x in equation (1) taken with the opposite sign:
k =
.
Again, according to Vieta's theorem, the sum of these roots is the coefficient at x in equation (1) taken with the opposite sign:
k =  +
+ 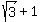 =
=  .
Answer. k =
.
Answer. k =  .
.
Solved. // Option C).