SOLUTION: A)A highway patrolman traveling at the speed limit is passed by a car going 20 mph faster than the speed limit. After one minute, the patrolman speeds up to 115 mph. How long afte

Algebra ->  Equations -> SOLUTION: A)A highway patrolman traveling at the speed limit is passed by a car going 20 mph faster than the speed limit. After one minute, the patrolman speeds up to 115 mph. How long afte      Log On


   

Question 1127250: A)A highway patrolman traveling at the speed limit is passed by a car going 20 mph faster than the speed limit. After one minute, the patrolman speeds up to 115 mph. How long after speeding up until the patrolman catches up with the speeding car. The speed limit is 55 mph.
B)Same question, but this time the patrolman speeds up to a speed of v mph (v>75).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
NOTE: Math problems often do not reflect real life. The patrolman could maintain speed for 1 minute, but it would take some time to accelerate to 115 mph, which is what we are supposed to assume.

AS A MATH PROBLEM:
As we expect the patrolman to catch up with the speedster in just a few minutes, we would define
t%22=%22 time, in minutes, from the time the speeding car passes the patrolman.

Case A:
As a function of time,
the distance covered by the speedster after that moment is
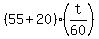%2855%2B20%29%28t%2F60%29 miles.
In the same time, the patrolman covers a distance (in miles) of
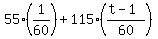55%281%2F60%29%2B115%28%28t-1%29%2F60%29 .
When the patrolman catches up with the speedster,
both will have covered the same distance since the speeding car passes the patrolman.
So, %2855%2B20%29%28t%2F60%29=55%281%2F60%29%2B115%28%28t-1%29%2F60%29 .
Multiplying both sides of the equal sign times 60 ,
the equation "simplifies' to
%2855%2B20%29t=55%2B115%28t-1%29 ,
75t=55%2B115t-115 ,
0=115t-75t-115%2B55 ,
0=40t-60 ,
60=40t
60%2F40=t
highlight%28t=1.5%29 .
So, the expected answer is that the patrolman catches up with the speedster
1.5 minutes after the speeding car passes the patrolman.

A CHECK:
In the initial first 1 minute the speedster covers
75%281%2F60%29=5%2F4=1.25 miles,
while the patrolman covers
55%281%2F60%29=11%2F12 miles.
In the next 0.5=1%2F2 minute, the speedster covers
%281%2F2%2975%281%2F60%29=5%2F8 miles,
while the patrolman covers
%281%2F2%29115%281%2F60%29=115%2F120=23%2F24 miles.
Total miles covered are
5%2F4%2B5%2F8=10%2F8%2B5%2F8=15%2F8 for the speedster, and
11%2F12%2B23%2F24=22%2F24%2B23%2F24=45%2F24=15%2F8 for the patrolman.

ANOTHER WAY TO THE SOLUTION:
In the initial first 1 minute the speedster gains a distance of
%2875-55%29%281%2F60%29=20%2F60=1%2F3 miles.
After that, the patrolman is 115-75=40 mph faster than the speedster,
and decreases the distance between both cars by
40%281%2F60%29=40%2F60=2%2F3 miles each minute.
At that rate it takes
%281%2F3%29%2F%282%2F3%29=%281%2F3%29%283%2F2%29=1%2F2 minutes
for the patrolman to catch up with the speedster.

Case B:
As a function of time,
the distance covered by the speedster after passing the patrolman is
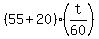%2855%2B20%29%28t%2F60%29 miles.
In the same time, the patrolman covers a distance (in miles) of
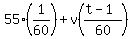55%281%2F60%29%2Bv%28%28t-1%29%2F60%29 .
When the patrolman catches up with the speedster,
both will have covered the same distance since the speeding car passes the patrolman.
So, %2855%2B20%29%28t%2F60%29=55%281%2F60%29%2Bv%28%28t-1%29%2F60%29 .
Multiplying both sides of the equal sign times 60 ,
the equation "simplifies' to
%2855%2B20%29t=55%2Bv%28t-1%29 ,
75t=55%2B75t-75 ,
0=vt-75t-v%2B55 ,
0=%28v-75%29t-v%2B55 ,
v-55=%28v-75%29t
%28v-55%29%2F%28v-75%29=t
highlight%28t=%28v-55%29%2F%28v-75%29%29 .
So, the expected answer is that the patrolman catches up with the speedster
%28v-55%29%2F%28v-75%29 minutes after the speeding car passes the patrolman.