Question 1116337: the fourth term of a GP is 1/2 and the sixth term is 1/8. its common ratio is negative
a) how many term of GP add up to give a sum of -2/22/32?
b)what is the sum to infinity for this GP
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ONE WAY TO START:
The recursive relation for a geometric progression,
relating term number  , ,  to the preceding term, to the preceding term, 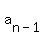 is is
 , where , where  is the common ratio. is the common ratio.
So, applying that to the fourth, fifth and sixth terms
 , ,
 , and , and
 --> -->  --> -->  . .
Knowing that  , we conclude that , we conclude that  , ,
and can write the first 4 terms, starting from the 4th,
and dividing by  (multiplying times -2) (multiplying times -2)
each time to get the term before:
 , ,
 , ,
 , ,
 . .
ANOTHER WAY:
The general "formula" for term number  , ,  , ,
of a GP with first term  and common ratio and common ratio  is is
 . .
Applying that to  , ,
 --> -->  --> -->  --> -->  --> --> 
AND FROM THERE:
The "formula" for the sum of the first  terms, terms,  , of a GP is , of a GP is

When  , ,
the term 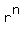 tends to tends to  as as  tends to tends to  , ,
and the sum to infinity is
 . .
In this case the sum to infinity is easy to calculate:
    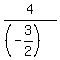  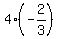  
Substituting the  and and  values found above, values found above,
the expression for the sum of the first  terms becomes terms becomes
  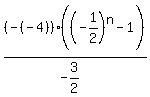  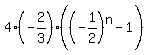  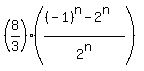  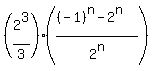  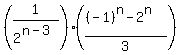
If that is supposed to be an irreducible fraction of the form 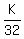 , ,
the only possibility is  , ,
and as  , ,  --> -->  . .
BOTH QUESTIONS WERE ANSWERED, BUT IF YOU WANT MORE,
knowing  , we could try to find that denominator. , we could try to find that denominator.
 . .
So,
   . .
|
|
|