Question 1116336: find a and b given that when x^3+2x^2+ax+6 is divided by x-1 the remainder is 4 and when divided by (x+2) the remainder is 16
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
This problem looks strange. It has only one unknown, but imposes two conditions on it.
So, formally, it is over constrained. Let's look into the solution.
The fact that x^3+2x^2+ax+6 gives the remainder of 4 when divided by x-1 means that the value of the polynomial at x= 1 is equal to 4
(according to the Remainder theorem):
1^3 + 2*1^2 + a*1 + 6 = 4, or
1 + 2 + a + 6 = 4, which implies
a = 4 - 1 - 2 - 6 = -5.
The fact that x^3+2x^2+ax+6 gives the remainder of 16 when divided by x+2 means that the value of the polynomial at x= -2 is equal to 16
(according to the Remainder theorem):
(-2)^3 + 2*(-2)^2 + a*(-2) + 6 = 16, or
-8 + 8 - 2a + 6 = 16, which implies
-2a = 16 + 8 - 8 - 6 = 10 ====> a = 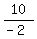 = -5.
Fortunately, both conditions give the same value for "a" equal to -5.
Answer. a = -5.
Notice. The condition says "find a and b", but the polynomial has only "a" and has no "b".
==============
On the Remainder theorem see the lessons
- Divisibility of polynomial f(x) by a binomial (x-a) and the Remainder theorem
- Solved problems on the Remainder theorem
- OVERVIEW of lessons on Divisibility of polynomial f(x) by binomial (x-a) and the Remainder theorem
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Divisibility of polynomial f(x) by binomial (x-a). The Remainder theorem".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
