Question 1110853: Find an interval over which the function f(x)=(x+5)^3(x-4)^2 is decreasing.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The interval over which the function  is decreasing is decreasing
is the interval where its derivative is negative.
 can be considered to be the product of the functions can be considered to be the product of the functions
 and and 
You must have learned that for a product function  , ,
the derivative 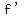 can be calculated can be calculated
from the factor functions,  and and  , ,
and their derivatives, 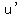 and and 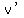 , as , as
 . .
In this case,  and and  , so , so

The zeros of that derivative are  , ,  and and  . .
Because  has even multiplicity has even multiplicity
(multiplicity is 2 because (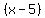 is squared). is squared).
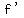 does not change sign at does not change sign at  . .
the derivative changes sign at the other two roots,
and it is obviously positive for  , ,
so it is negative only in the interval  . .
|
|
|