.
The way is THIS:
Consider the system of 2 equations
y = 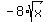 , (1)
y - (-4) = m(x-4). (2)
It is the same, as the system
y =
, (1)
y - (-4) = m(x-4). (2)
It is the same, as the system
y = 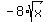 , (1)
y + 4 = m(x-4). (2)
Find the slope "m" under the condition that the system has a UNIQUE solution (x,y) = (4,-4).
For it, substitute expression for y, y = m*(x-4)-4 into equation (1). You will get
m*(x-4) + 4 =
, (1)
y + 4 = m(x-4). (2)
Find the slope "m" under the condition that the system has a UNIQUE solution (x,y) = (4,-4).
For it, substitute expression for y, y = m*(x-4)-4 into equation (1). You will get
m*(x-4) + 4 = 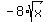 . (*)
Introduce new variable u =
. (*)
Introduce new variable u =  . Then the equation (*) takes the form
. Then the equation (*) takes the form
 =
= 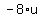 ,
,
 =
= 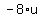 ,
,
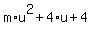 = 0. (**)
The condition that the equation (**) has a unique solution in "u" means that the discriminant of the equation (**) is equal to zero.
Write the discriminant of the quadratic equation (**) and equate it to zero:
d =
= 0. (**)
The condition that the equation (**) has a unique solution in "u" means that the discriminant of the equation (**) is equal to zero.
Write the discriminant of the quadratic equation (**) and equate it to zero:
d =  =
= 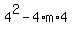 = 16 - 16m ====>
the equation d = 0 becomes 16 - 16m = 0, which implies 16m = 16 ====> m = 1.
Answer. The slope under the question is m= 1,
found without using derivatives.
= 16 - 16m ====>
the equation d = 0 becomes 16 - 16m = 0, which implies 16m = 16 ====> m = 1.
Answer. The slope under the question is m= 1,
found without using derivatives.