Question 1105912: How many ordered pairs of positive integers (x,y) satisfy the equation  ?
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! How many ordered pairs of positive integers (x,y) satisfy the equation
x(y^2-x) = 4 - x
xy^2 - x^2 = 4 - x
xy^2 = x^2 - x + 4
y^2 = 
y =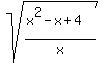 
and
y =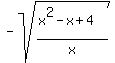 
plot these two equations
:
4 pairs of integers: 1,2; 4,2; 1,-2, 4,-2, however when x = 4, it does not hold up in the original equation so only two pairs: 1,2; 1,-2
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
x =  ====>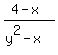
x(y^2-x) = 4 - x
xy^2 - x^2 = 4 - x
xy^2 = x^2 - x + 4
y^2 =
y^2 = x - 1 +  . (1)
y is integer. So, y^2 is integer. x is integer. So, (x-1) is integer.
It implies that "x" is the solution to the problem if and only if the value is positive integer.
It implies, in turn, that "x" may have only these values: x= 1, 2 and/or 4.
Then from (1) y^2 = 4, 3 and 1, respectively.
In order for "y" be integer, y^2 can not be 3.
So, only one pair is the solution: (x,y) = (1,2).
|
|
|
