SOLUTION: if (a*a)+(b*b)=29 and ab=10 then find the values of a and b please explain how to solve

Algebra ->  Equations -> SOLUTION: if (a*a)+(b*b)=29 and ab=10 then find the values of a and b please explain how to solve       Log On


   

Question 1105730: if (a*a)+(b*b)=29 and ab=10 then find the values of a and b
please explain how to solve
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
system%28a%5E2%2Bb%5E2=29%2Cab=10%29


a%5E2%2B2ab%2Bb%5E2=29%2B2%2A10=49
a%5E2%2B2ab%2Bb%5E2=7%5E2
%28a%2Bb%29%5E2=7%5E2
a%2Bb=7

Revise the system:
system%28a%2Bb=7%2Cab=10%29


The numbers are 2 and 5.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Answer.   There are  4  solutions:   (a,b) = (5,2),  (2,5),  (-5,-2)  and  (-2,-5).

Solution 

a%5E2+%2B+b%5E2 = 29    (1)
ab     = 10    (2)


Multiply eq(2) by 2 and then add to eq(1).  You will get

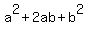a%5E2+%2B+2ab+%2B+b%5E2 = 29+2*10 = 49,   or

%28a%2Bb%29%5E2 = 49.


Take square root of both sides. You will get

a + b = +/- sqrt%2849%29 = +/- 7.


Case 1:

    a + b =  7,     (3)
    ab    = 10.     (4)


    From (3), express a = 7-b  and substitute it into (4), replacing "a":

    (7-b)*b = 10  ====>  7b - b^2 = 10  ====>  b^2 - 7b + 10 = 0  ====>

                         factor left side:  (b-5)*(b-2) = 0.

    It gives two roots: b= 5  or  b= 2.

    If b= 5, then from (3)  a = 2.  

    If b= 2, then from (3)  a = 5.


    In this way you get the first two answers.



Case 2:

    a + b = -7,     (5)
    ab    = 10.     (6)


Do the same to get the third and the fourth answers.

Solved.