Question 1103463: When a natural number n is divided by the numbers 95, 112, 214 and 231, they all leave the same remainder. What is n?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
Let N be the number under the question, and let "r" be the remainder.
Then the number N-r is multiple of all numbers 95, 112, 214 and 231.
95 = 5*19;
112 =  ;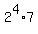
214 = 2*107;
231 = 3*7*11.
Hence, N-r is a multiple of the LCM (Less Common Multiple) of the numbers 95, 112, 214 and 231, which is 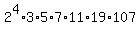 = 37569840.
So, the answer is: any number of the form N = 37569840*k + r
with the arbitrary integer "k" and "r" (0 <= r < 95) satisfies to the given condition.
The least such a positive integer number is 1 (one; ONE).
The next such a positive integer number is 2 (two; TWO).
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
As tutor ikleyn showed, the problem as you show it is not very interesting, because it has an infinite number of solutions.
So I'm wondering if, perhaps due to a language difficulty, you stated the problem incorrectly.
I suspect the problem was supposed to say that, when the numbers 95, 112, 214, and 231 are divided by a natural number n, the remainders are all the same.
If that is the case, the problem is much easier to solve.
The differences between any two of the given numbers are all multiples of 17, so the answer would be that n is 17.
That is, the numbers 95, 112, 214, and 231, when divided by 17, all leave the same remainder, 10.
Is that by chance what the problem was supposed to be?
|
|
|
