SOLUTION: I have this exponential equation that I cannot seem to solve: 5^x = 4^x+1 I didn't get very far; here's my lame attempt: log5^x = log4^x+1 xlog5 = (x+1) log4 and that'

Algebra ->  Equations -> SOLUTION: I have this exponential equation that I cannot seem to solve: 5^x = 4^x+1 I didn't get very far; here's my lame attempt: log5^x = log4^x+1 xlog5 = (x+1) log4 and that'      Log On


   

Question 1103116: I have this exponential equation that I cannot seem to solve:
5^x = 4^x+1
I didn't get very far; here's my lame attempt:
log5^x = log4^x+1
xlog5 = (x+1) log4
and that's about it. I don't know if I should distribute the log4 over the (x+1) or what. I know the answer is log4/log5/4 ("log 4 divided by log 5/4"), but I don't know how to get there. Can you help?
Thank you

Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


(Note that the given equation, as you show it, is 5^x = 4^x + 1, or 5%5Ex+=+4%5Ex%2B1; that is much different than the equation you are really trying to solve, which is 5^x = 4^(x+1), or 5%5Ex+=+4%5E%28x%2B1%29. As another tutor on this site likes to say, "parentheses are free -- use them!")

You have done all you can do with the logarithms; now you have an equation in just x which you can solve.

Yes; distribute. Then solve for x (hint gather all the terms with x on one side of the equation).

Then note that the given answer, 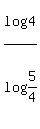log%284%29%2Flog%285%2F4%29, can be written, using laws of logarithms, as log%284%29%2F%28log%285%29-log%284%29%29.

When you finish solving your equation for x, that is exactly what you should get.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
If the equation is 

5%5Ex = 4%5Ex + 1,


then the solution is x= 1.





Plot y = 5%5Ex (red)  and  y = 4%5Ex%2B1 (green)