SOLUTION: Please help me to solve the following problem. The following equation must be shown to have no solution: 2x^4+2y^4=z^4 I have come to realize that this equation is a diophantos

    STATEMENT:

        If   + 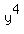 =  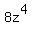 and x, y and z are integer numbers, then both  x  and  y are even numbers.


PROOF of the statement.


For the proof, present  x = 8m + i,  y = 8n + j,  where 0 <= i <=7,  0 <= j <= 7.
 
Then write

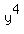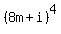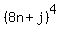     +  =  +  = (use the binomial formula) = (sum of the terms multiple of 8) +  + .


Below I prepared a rectangular table containing  the numbers 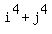  mod 8  with two entries  and 


The table has two entries columns at the left and two entries rows at the top:


		1	2	3	4	5	6	7	<<< j
i   i^4 mod 8	1	0	1	0	1	0	1	<<< j^4 mod 8
1	1	2	1	2	1	2	1	2	
2	0	1	0	1	0	1	0	1	
3	1	2	1	2	1	2	1	2	
4	0	1	0	1	0	1	0	1	
5	1	2	1	2	1	2	1	2	
6	0	1	0	1	0	1	0	1	
7	1	2	1	2	1	2	1	2


The most left column simply lists the numbers  (remainders)  i = 1, 2, 3, 4, 5 , 6, 7 (mod 8).
The next column contains the number (remainders)   mod 8.

The most upper row lists the numbers  (remainders)  j = 1, 2, 3, 4, 5 , 6, 7 (mod 8).
The second row contains the number (remainders)   mod 8.

The table itself contains, as I just said, the sums 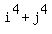  mod 8.

From the table you can see that 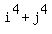  is multiple of 8 if and only if BOTH i and j are EVEN numbers. 
                                                                    (Then and only then we have 0 (zero) in the Table).

Thus the lemma is proved.

Let the numbers x, y and z are the solution in integer numbers to the given equation:

 + = .


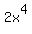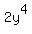Then the left side is an even number.
Hence, right side is an even number.
Then   is an even number.
It implies that z itself is an even number:  z = 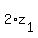, where  is integer.

Then the given equation can be written in the form

 +  = .

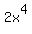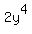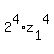Reduce/(cancel) the factor 2 in both sides.  You will get

 +  = .


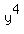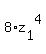Now, according to the lemma,  both x and y are even numbers.


This chain of arguments opens the way for the "infinite descent" method.

     (The method is attributed to Pierre Fermat and was used by Leonard Euler).

Let assume that equation 

 + = 

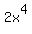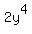has the solution in integer numbers and the triple (x,y,z) IS the solution.


It is clear that if all three numbers x, y and z are even, we can cancel all the three numbers by this common divisor 2, 
and the new triple also will be the solution to the same equation.


We will cancel this common divisor 2 as many times as possible.

Finally, we can assume that we got (we have) the triple, in which NO MORE THAN ONE member of "x" and "y" is multiple of 2.

     (If BOTH "x" AND "y" ARE multiples of 2, then obviously the third number z is also multiple of 2 - the case which we just EXCLUDED).

OK. So, let us assume first that no one of the three terms x, y, z is multiple of 2.


But the LEMMA IMPLIES that BOTH x and y are even numbers.


          CONTRADICTION.


OK. So, let us assume next that only one of the two terms  "x"  and  "y"  is multiple of 2.


But the LEMMA IMPLIES again that BOTH x and y are even numbers.


          CONTRADICTION.