Question 1100461: How am i to get the solution to the equation |x-3|=2x+1?
It says I am to end up with a extraneous solution, but I do not know what that means or how to get it.
Found 3 solutions by Alan3354, KMST, ankor@dixie-net.com:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! How am i to get the solution to the equation |x-3|=2x+1?
------------
x-3 = 2x+1
x = 2x + 4
-x = 4
x = -4
Check:
|-4-3| = -7
|-7| = -7
NG
Absolute value cannot be negative.
--> extraneous solution
===============
-(x-3) = 2x+1
-x+3 = 2x+1
3 = 3x+1
3x = 2
x = 2/3
=================
Check:
|x-3|=2x+1
|(2/3 - 3)| = 4/3+1 = 7/3
|-7/3| = 7/3
No problem.
---------------------
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Maybe  , and then , and then  , ,
or maybe 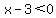 and then and then  . .
If 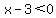 , ,
the equation simplifies to
 <--> <-->  <--> <-->  <--> <-->  <--> <-->  . .
That is a solution of  , ,
but is it a solution of the original equation?
Let's check.
If  , ,  and and  . .
At the same time, if  , ,  . .
Clearly,  makes makes  true, true,
so  is a solution of is a solution of  . .
What about the case when  ? ?
Will that lead to another solution?
If  , ,
the equation simplifies to
 <--> <-->  <--> <-->  . .
 is a solution to is a solution to  , ,
but it is not a solution to the original equation.
It makes  , ,  , and , and
 . .
Clearly, if  makes makes  , and , and  , ,
it is not a solution to  . .
we call it an extraneous solution.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! |x-3| = 2x+1
x - 3 = 2x + 1
-3 - 1 = 2x - x
-4 = x, an extraneous solution, as you can see if you substitute in the original equation
|-4 - 3| = 2(-4) + 1
|-7| = -8 + 1
Absolute is always positive
+7 does not = -7
:
Solution 2
|x - 3| = 2x + 1
x - 3 = -(2x + 1)
x - 3 = -2x - 1
x + 2x = -1 + 3
3x = 2
x = 2/3, this solution will work in the original equation
:
|(2/3)-3)| = 2(2/3) + 1
|- 7/3| = +7/3
+7/3 = +7/3
|
|
|