Question 1097215: A toy making company has at least 300 squares of felt, 700 oz of stuffing, and 230 ft of trim to make dogs and dinosaurs. A dog uses 1 square of felt, 4 oz of stuffing, and 1 ft of trim. A dinosaur uses 2 squares of felt, 3 oz of stuffing, and 1 ft of trim.
It costs the company $1.65 to make each dog and $1.52 for each dinosaur. What is the company's minimum cost?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of dogs
y = number of dinosaurs
total cost = 1.65 * x + 1.52 * y
this is your objective function and what you want to minimize.
each dog requires 1 square of felt, 4 ounces of stuffing, and 1 foot of trim.
each dinosaur requires 2 squares of felt, 3 ounces of stuffing and 1 foot of trim.
you have available:
at least 300 squares of felt
at least 700 ounces of stuffing.
at least 230 feet of trim.
your constraint equations are:
x + 2y >= 300
4x + 3y >= 700
x + y >= 230
since you only have two unknown variables, you can solve this graphically.
if you graph the opposite of these inequalities, then the area of the graph that is not shaded is your region of feasibility.
the corner points of this region of feasibility contain your minimum cost.
you evaluate your cost at these corner points and the coordinate pair that contains the lowest cost is your solution.
the following graph shows you what the corner points are.
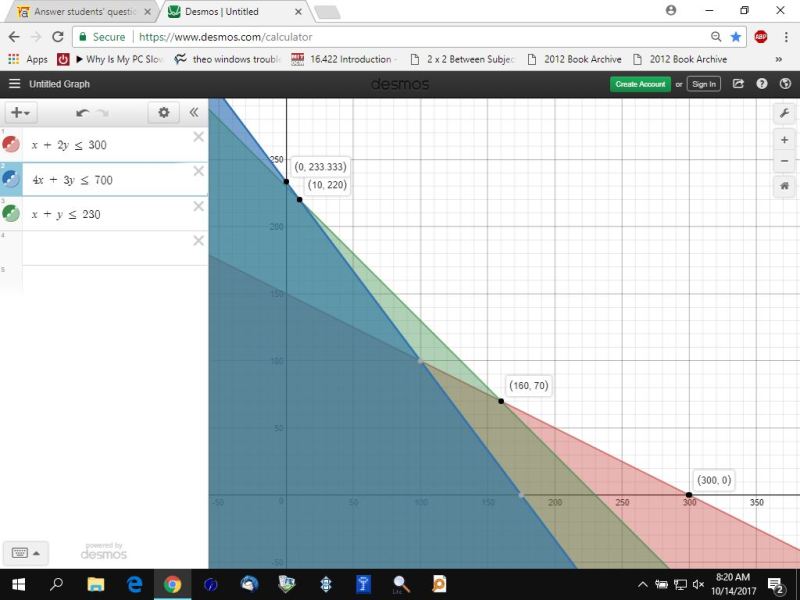
your cost at each of these corner points is the evalution of 1.65 * x + 1.52 * y.
at (300,0), the cost is 495.
at (160,70), the cost is 370.4
at (10,220), the cost is 350.9
at (0,233 + 1/3), the cost is 354.67.
your minimum cost is at (10,220) which means you would make 10 dogs and 220 dinosaurs.
at (10,220), your constraints equations need to be satisfied as well.
they are:
x + 2y >= 300 becomes 10 + 2 * 220 = 10 + 440 = 450 >= 300 therefore satisfied.
4x + 3y >= 700 becomes 4 * 10 + 3 * 220 = 700 >= 700 therefore satisfied.
x + y >= 230 becomes 10 + 220 = 230 >= 230 therefore satisfied.
minimum cost at (10,220) and all constraints are satisfied, therefore good.
|
|
|