Question 1092731: May I have some help with this question please? I have to solve the equation and inequality and show all steps and work. It's one homework problem from the summer and I am still not clear on it. The "0" is confusing to me.
(x-3)/(x+2) > 0 USE INTERVAL NOTATION
Thanks.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! looking at this function on the graph will help you to see what's going on.
here's the graph of y = (x-3) * (x+2)
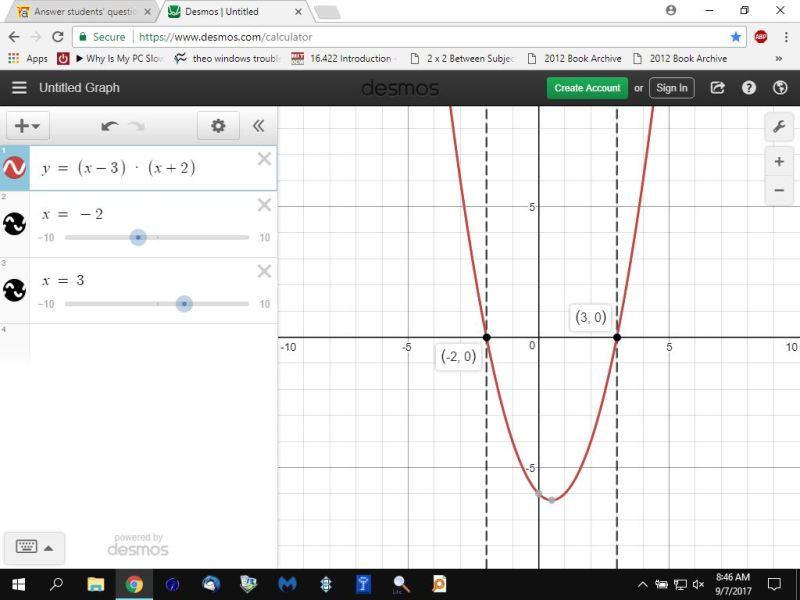
you can see that the graph crosses the x-axis at x = -2 and x = 3.
that's where the value of y is equal to 0.
when y = 0, the equation becomes 0 = (x-3) * (x+2)
y is equal to 0 when x = 3 because y = (3-3) * (3+2) which is equal to 0 * 6 which is equal to 0.
y is equal to 0 when x = -2 because y = (-2-3) * (-2+2) which is equal to 6 * 0 which is equal to 0.
those are the roots of the equation and are found when you you set y = 0 in the equation of y = (x-3) * (x+2).
you are asked to find the value of x when (x-3) * (x+2) > 0.
if you set y = (x-3) * (x+2), then the question is to find the value of x when y > 0, because y = (x-3) * (x+2).
y is used to represent the equation because we normally graph a 2 dimensional equation with x on the horizontal axis and y on the vertical axis.
it doesn't have to be that way, but most of the graphing software is set up that way.
some more sophisticated graphing software allow you to use any variable name you want, but those capabilities are not always available.
for example, the ti-84 plus requires the vertical axis to be the value of y, while the horizontal axis requires the horizontal axis to be x.
if you're familiar with functional notation, then the equation would have been shown as f(x) = (x-3) * (x+2).
the use of f(x) and y are inter-changeable as they both represent the value of the equation after replacing the x variable with a value.
if you were using f(x) = (x-3) * (x+2), then the question would have been to find the value of x when f(x) > 0.
so, .....
you can find the answer to this problem by setting y = (x-3) * (x+2) and then graphing it and finding out where it crosses the x-axis.
this will be at x = -2 and x = 3.
you would then test the intervals where x < -2 and -2 < x < 3 and x > 3 to see if the function is positive or negative in those intervals.
you can see that the function is positive when x < -2 and when x > 3, and that the function is negative when -2 < x < 3.
that's your answer graphically.
if you were to do the same without the benefit of looking at a graph, you would solve in a similar way.
you would make your equation y = (x-3) * (x+2) and then set y = 0 to find the roots.
the equation would be 0 = (x-3) * (x+2)
this is a quadratic equation because when you multiply the factors out, the leading term is x^2.
in fact, the quadratic equation, before being factored, is y = x^2 - x - 6.
factor that equation and you get y = (x-3) * (x+2)
since it's already in factored form, it's easy to see that the roots of the equation are x = 3 and x = -2.
that's when y = 0.
the rest is finding the interval when y is positive, which means when (x-3) * (x+3) is positive.
since the function is continuous, if any point in the interval is positive, then all points in the interval will be positive until the function crosses the x-axis.
likewise if any point in the interval is negative.
it will remain negative until the function crosses the x-axis again.
so just test a point in each interval and it will tell you whether that interval is positive or not.
the intervals to test are:
x < -2
-2 < x < 3
x > 3
those are what are called the critical points in the graph which is the points where the function can change sign.
there is a third way to look at it.
you want to know when the function (x-3) * (x+2) is greater than 0.
if you let a = (x-3) and b = (x+2), then the function becomes a * b > 0
this occurs when a and b are both positive and when a and b are both negative.
so, you are looking for when (x-3) is positive and when (x+2) is positive, and you are looking for when (x-3) is negative and when (x+2) is also negative.
take a look at (x-3)
it is positive when x > 3
it is negative when x < 3
take a look at (x+2)
it is positive when x > -2
it is negative when x < -2
so, positive * positive is when x > 3 or x > -2.
and, negative * negative is when x < 3 or x < -2
if you want to have the factors both positive at the same time, then it can only occur when x > 3.
it is possible for x > -2 and not > 3, but it is not possible for x > 3 and not > -2.
likewise, if you want to have the factors both negative at the same time, then it can only occur when x < -2.
it is possible for x < 3 and not < -2, but it is not possible for x < -2 and not < 3.
in all of this, you should wind up with the same conclusion.
(x-3) * (x+2) > 0 when x < -2 and when x > 3.
in interval notation this would be x = (-infinity, -2) union (3, infinity)
Answer by ikleyn(52777)  (Show Source):
You can put this solution on YOUR website! .
There are 2 (two) critical points: x= 3, where the numerator becomes equal to zero, and x= -2, where the denominator becomes equal to zero.
And there are 3 (three) intervals on the number line:
1)  < x < -2,
2) -2 < x < 3, and
3) 3 < x <  .
On the interval 1) both the numerator and denominator are negative; so, the left side rational function is positive.
On the interval 2) the denominator is positive, while the numerator is negative. So, the left side rational function is negative.
On the interval 3) both the numerator and denominator are positive. So, the left side rational function is positive.
Conclusion. The solution to the given inequality is the UNION of two intervals (-infinity,-2) U (3,infinity).
See the plot below as an illustration.
Plot y =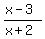 
This is the standard way and the sample/template on how the solution of similar problems should be made and presented (as mantra . . . )
See the lesson
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
in this file.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Inequalities".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
