SOLUTION: x^2 + xy = 20 y^2 + xy = 30 xy = ?

Algebra ->  Equations -> SOLUTION: x^2 + xy = 20 y^2 + xy = 30 xy = ?       Log On


   

Question 1089783: x^2 + xy = 20
y^2 + xy = 30
xy = ?


Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
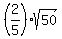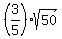One solution is      x = %282%2F5%29%2Asqrt%2850%29,   y = %283%2F5%29%2Asqrt%2850%29.


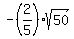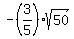Another solution is  x = -%282%2F5%29%2Asqrt%2850%29,  y = -%283%2F5%29%2Asqrt%2850%29.


In both cases  xy = 12.


If you want to get "the steps", send me your message through the TY notes.
In this case refer to the ID number of this problem, which is 1089783,
in order for I could identify the problem.

And do not forget to send your thanks to me.

-------
Comment from student: Thank you. Please send me the steps.
-------

-------
My response: OK. See the solution below.
------- 

x^2 + xy = 20,    (1)
y^2 + xy = 30.    (2)

Add equations (1) and (2) . You will get

x^2 + 2xy + y^2 = 20 + 30,   or, which is the same,   %28x%2By%29%5E2 = 50.

Take the square root from both sides. You will get

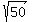x + y = +/- sqrt%2850%29.   (3)


First, let us consider the case 

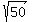x + y = sqrt%2850%29.       (4)


Distract equation (1) from equation (2). You will get

y^2 - x^2 = 30 - 20,    or, which is the same,

(y-x)*(y+x) = 10.               (5)


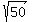Substitute sqrt%2850%29 instead of (y+x) into (5), based on (4). You will get

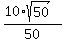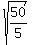y - x = 10%2Fsqrt%2850%29 = %2810%2Asqrt%2850%29%29%2F50 = sqrt%2850%2F5%29.    (6)


Now you have these two equations

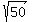x + y = sqrt%2850%29     (7)    ( from (4) )

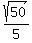y - x = sqrt%2850%29%2F5.    (8)    (from (6) )


Add the two equations (7) and (8). You will get

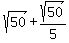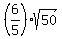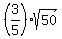2y = sqrt%2850%29+%2B+sqrt%2850%29%2F5 = %286%2F5%29%2Asqrt%2850%29  ====>  y = %283%2F5%29%2Asqrt%2850%29.

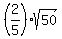Then from (7) you can easily get  x = %282%2F5%29%2Asqrt%2850%29.


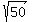Thus we completed the case  x + y = sqrt%2850%29. 


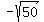Working similarly, you can consider the case   x + y = -sqrt%2850%29


Then you will get the second answer mentioned above.

Solved.