Question 1089048: for what value of a does the quadratic function f(x)=ax^2-6x+3 have no
x-intercepts?
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52778)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! An  -intercept is the point where a parabola crosses the x-axis. This point is also known as a -intercept is the point where a parabola crosses the x-axis. This point is also known as a  , ,  , or , or  . .
the expression  , called the " , called the " ", and we can use it to find out what kind and how many roots the quadratic function have ", and we can use it to find out what kind and how many roots the quadratic function have
rule:
if 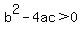 , Discriminant is greater than zero, Positive Discriminant: , Discriminant is greater than zero, Positive Discriminant: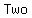 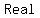 Solutions Solutions
if  , Discriminant is equal to zero. , Discriminant is equal to zero. 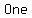 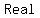 Solution Solution
if 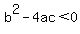 , Discriminant is less than zero ,Negative Discriminant: , Discriminant is less than zero ,Negative Discriminant:  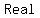 Solutions => means Solutions => means   -intercepts -intercepts
so, you will use 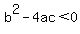 for for 
since  , ,  , and , and  , you have , you have
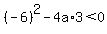
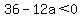

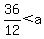
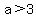
check:
if 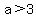 , we can use , we can use  and see the graph of and see the graph of 

as you can see, there is no x-intercept
|
|
|