Question 1079291: Please help me solve this
Suppose the quantity Q, in mg, of medicine in a patientís bloodstream is decreasing by 25% each 40 minutes. Let us write Q = f(T), where T is in minutes since the injection of medicine. Suppose the injection contains 300 mg of medicine.
(a) Construct a table of values for Q as a function of T over a few hours.
(b) Find a formula for f in the form A ◊ B^T, or an equivalent form.
(c) Let th be the time taken for the quantity of medicine in the bloodstream to halve. By a process of guessing and checking, estimate the value of Th (accurate to 3 significant figures).
(d) Determine the exact value of Th.
(e) Show that the halving time is constant. That is, show that starting from an arbitrary time
T= a, the quantity of medicine is halved after an additional time Th.
(f) Sketch a graph of the function over a 4 hour period since the injection.
(g) The patient can receive a new injection when the quantity of medicine is less than 2% of the original dose. For simplicity, this time delay is measured in a whole number of hours. Determine the wait time. For medicinal safety, should we round up or down to the nearest hour?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the interest rate per time period.
n is the number of time periods.
the quantity of medicine is decreasing by 25% every 40 minutes.
your time period is therefore every 40 minutes.
your rate is -25% every 40 minutes.
in the formula, you use the decimal equivalent of the percent which is equal to the percent / 100.
the interest rate per time period is therefore -.25
the formula of f = p * (1 + r) ^ n becomes
f = p * (1 - .25) ^ n which becomes:
f = p * .75 ^ n
in order for the value of the medicine to be equal to 1/2 what it was, the formula becomes:
1/2 = .75^n
this is because f is 1/2 and p is 1, and 1 * .75 ^ n is the same as .75 ^ n.
you would solve for n using logs.
take the log of both sides of the eqution to get log(1/2) = log(.75^n)
because log(b^n) = n*log(b), this becomes:
log(1/2) = n*log(.75)
divide both sides of this equation by log(.75) and you get:
log(1/2) / log(.75) = n
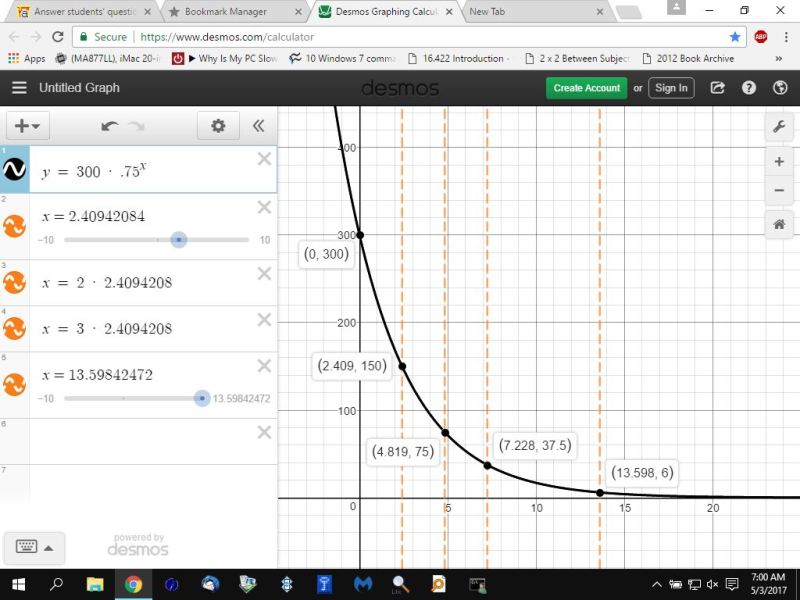
solve for n to get n = 2.40942084
this means that that the original amount will be half of what it was in 2.40942084 time periods that are 40 minutes each.
translate this to minutes, and it becomes n = 2.40942084 * 40 = 96.37683359 minutes.
this formula will work regardless of the value of the milligrams in the blood stream.
start with 300 mg
you will have 150 mg in the blood stream in 2.40942084 time periods.
f = 300 * .75 ^ 2.40942084 = 150
f = 150 * .75 ^ 2.40942084 = 75
f = 75 * .75 ^ 2.40942084 = 37.5
etc.
the amount of drug in the bloodstream will be half of what it was every 2.40942084 time periods.
your original table can be set up in 40 minute intervals.
when n = 0, the value in this table will be 300 * .75 ^ 0 = 300.
when n = 1, the value in this table will be 300 * .75 ^ 1 = 225
when n = 2, the value in this table will be 300 * .75 ^ 2 = 168.75
when n = 3, the value in this table will be 300 * .75 ^ 3 = 126.5625
etc.
for the remaining dose being 2% of the original dose, you would calculate the time required in 40 minute intervals as follows:
2% of 300 = .02 * 300 = 6 mg.
in the formula of f = p * .75 ^ n, you would get:
6 = 300 * .75 ^ n
you will want to solve for n in this equation.
divide both sides of the equation by 300 to get:
6/300 = .75 ^ n
take the log of both sides of this equation to get:
log(6/300) = log(.75^n)
this becomes log(6/300) = n * log(.75)
divide both sides of the equation by log(.75) to get:
log(6/300) / log(.75) = n
solve for n to get n = 13.59842472
the original dose of 300 mg should reduce to 6 mg in 13.59842472 time periods that are 40 minutes each.
that's equivalent to 13.59842472 * 40 = 543.9369888 minutes which is equivalent to 543.9369888 / 60 = 9.06561648 hours.
to be on the safe side, you would round down so there is at least 2% of the medicine in the bloodstream.
to graph the equation, replace f with y and replace n with x to get:
y = 300 * .75^x
your graph will look like this:
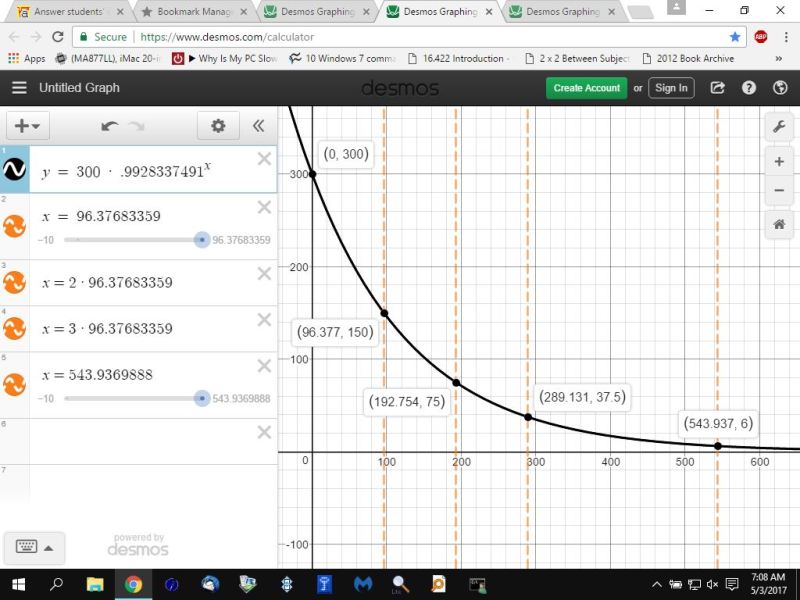
if your want your time intervals to be minutes instead of 40 minutes, you would do the following.
.75 ^ 1/40 = .9928337491
your growth rate per minute would be .9928337491 per 1 minute interval.
your time interval is now in minutes.
i will graph the equation of y = 300 * .9928337491 ^ x to show you that this is equivalent to the same equation when the time period is in 40 minute intervals.
your graph looks like this.
the value of x is now every minute rather than every 40 minutes.
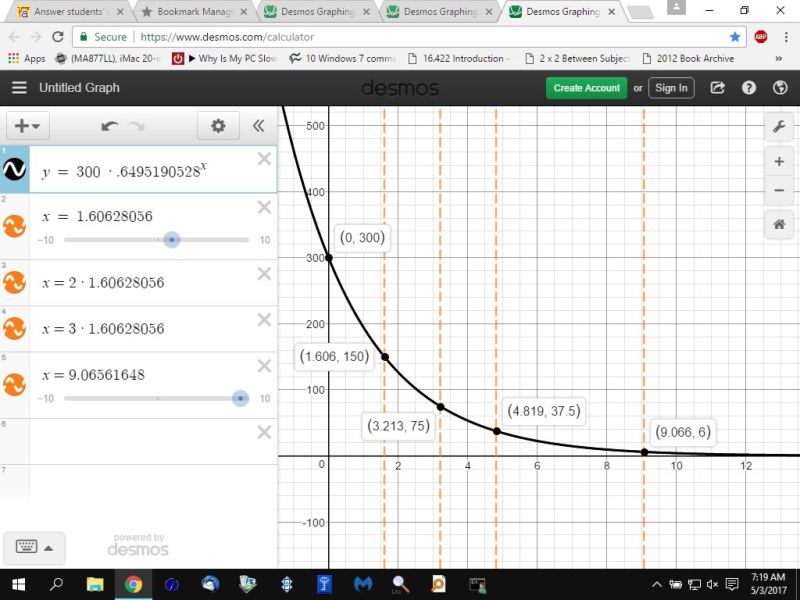
you can also translate to hours.
your do that as follows:
hours relative to 40 minutes are 60/40 = 6/4 = 3/2
.75 ^ (3/2) = .6495190528
your equation becomes y = 300 * .6495190528 ^ x
the value of x is now every hour instead of every 40 minute interval.
the graph of that equation looks like this:
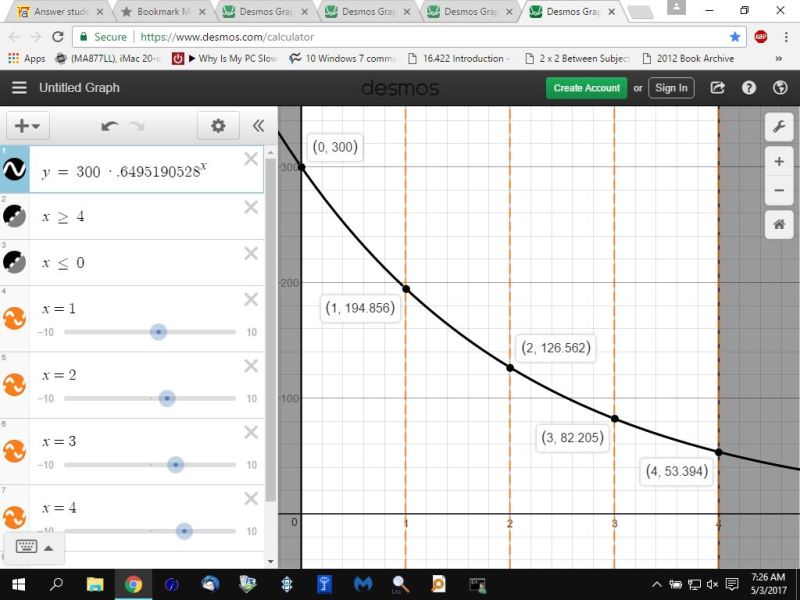
if you want to sketch a 4 hour graph, it would look like this:
|
|
|