

 A quadratic equation with 0 on the right has two
real roots if the discriminant > 0
We find the discriminant which is
A quadratic equation with 0 on the right has two
real roots if the discriminant > 0
We find the discriminant which is  here a=1, b=b, c=
here a=1, b=b, c=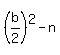 So the discriminant is
So the discriminant is
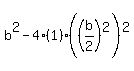 which we set
which we set 
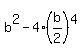

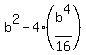

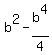
 Multiply through by 4
Multiply through by 4
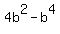
 Factor out b2
Factor out b2
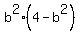

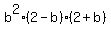
 The critical numbers are 0,2 and -2.
[The critical numbers all cause the discriminant to = 0,
which gives the quadratic only one real solution.
So none of the critical numbers are possible values
for b.
We place the critical numbers on a number line
---------o-------o-------o--------
-4 -3 -2 -1 0 1 2 3 4
We test values in each interval:
Using test value -3 for the first (leftmost) interval
The critical numbers are 0,2 and -2.
[The critical numbers all cause the discriminant to = 0,
which gives the quadratic only one real solution.
So none of the critical numbers are possible values
for b.
We place the critical numbers on a number line
---------o-------o-------o--------
-4 -3 -2 -1 0 1 2 3 4
We test values in each interval:
Using test value -3 for the first (leftmost) interval
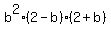

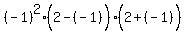






 That's true so we shade the interval (-2,0).
---------o=======o-------o--------
-4 -3 -2 -1 0 1 2 3 4
Using test value 1 for the next interval
That's true so we shade the interval (-2,0).
---------o=======o-------o--------
-4 -3 -2 -1 0 1 2 3 4
Using test value 1 for the next interval
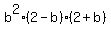

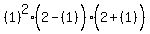






 That's true so we also shade the interval (0,2).
---------o=======o=======o--------
-4 -3 -2 -1 0 1 2 3 4
Using test value 3 for the next interval
That's true so we also shade the interval (0,2).
---------o=======o=======o--------
-4 -3 -2 -1 0 1 2 3 4
Using test value 3 for the next interval
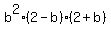

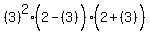

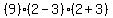




 That's false. Therefore b must be in these intervals
in order for the equation to have 2 real roots:
(-2,0) U (0,2)
Edwin
That's false. Therefore b must be in these intervals
in order for the equation to have 2 real roots:
(-2,0) U (0,2)
Edwin