.
I read your problem in THIS way:
If ( ,
, , . . .
, . . .  ) satisfy
) satisfy
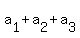 = 1,
= 1,
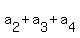 = 2,
= 2,
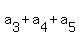 = 3,
. . . . . . . . . <<<---=== I added THIS which means that there are similar equations for all intermediate indexes
= 3,
. . . . . . . . . <<<---=== I added THIS which means that there are similar equations for all intermediate indexes
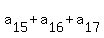 = 15,
= 15,
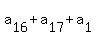 = 16,
= 16,
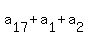 = 17
what is the value of
= 17
what is the value of  ?
?
~~~~~~~~~~~~~
Below is the system of equations written in full
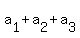 = 1, (1)
= 1, (1)
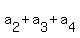 = 2, (2)
= 2, (2)
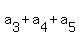 = 3, (3)
= 3, (3)
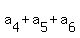 = 4, (4)
= 4, (4)
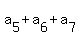 = 5, (5)
= 5, (5)
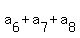 = 6, (6)
= 6, (6)
 = 7, (7)
= 7, (7)
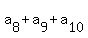 = 8, (8)
= 8, (8)
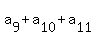 = 9, (9)
= 9, (9)
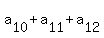 = 10, (10)
= 10, (10)
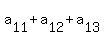 = 11, (11)
= 11, (11)
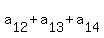 = 12, (12)
= 12, (12)
 = 13, (13)
= 13, (13)
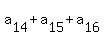 = 14, (14)
= 14, (14)
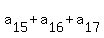 = 15, (15)
= 15, (15)
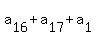 = 16, (16)
= 16, (16)
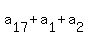 = 17. (17)
Add all 17 equations (1) - (17) (both sides). You will get
= 17. (17)
Add all 17 equations (1) - (17) (both sides). You will get
 = 1 + 2 + 3 + . . . + 15 + 16 + 17 =
= 1 + 2 + 3 + . . . + 15 + 16 + 17 = 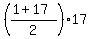 = 9*17 = 153.
Now divide both sides of the lest equation by 3, and you will get
= 9*17 = 153.
Now divide both sides of the lest equation by 3, and you will get
 = 51. (18)
Next subtract equation (1) from the equation (18). You will get
= 51. (18)
Next subtract equation (1) from the equation (18). You will get
 = 51 - 1 = 50. (19)
Next subtract equation (4) from the equation (19). You will get
= 51 - 1 = 50. (19)
Next subtract equation (4) from the equation (19). You will get
 = 50 - 4 = 46. (20)
Next subtract equation (7) from the equation (20). You will get
= 50 - 4 = 46. (20)
Next subtract equation (7) from the equation (20). You will get
 = 46 - 7 = 39. (21)
Next subtract equation (10) from the equation (21). You will get
= 46 - 7 = 39. (21)
Next subtract equation (10) from the equation (21). You will get
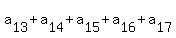 = 39 - 10 = 29. (22)
Next subtract equation (13) from the equation (22). You will get
= 39 - 10 = 29. (22)
Next subtract equation (13) from the equation (22). You will get
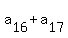 = 29 - 13 = 16. (23)
Now compare equations (23) and (16). You instantly will get
= 29 - 13 = 16. (23)
Now compare equations (23) and (16). You instantly will get
 = 16 - 16 = 0. (24)
Having known
= 16 - 16 = 0. (24)
Having known  = 0, we can rewrite the equation (18) in the form
= 0, we can rewrite the equation (18) in the form
 = 51. (25)
= 51. (25)
Now we are on the finish line, finally !!!
Next subtract equation (2) from the equation (25). You will get
 = 51 - 2 = 49. (26)
Next subtract equation (5) from the equation (25). You will get
= 51 - 2 = 49. (26)
Next subtract equation (5) from the equation (25). You will get
 = 49 - 5 = 44. (27)
Next subtract equation (8) from the equation (27). You will get
= 49 - 5 = 44. (27)
Next subtract equation (8) from the equation (27). You will get
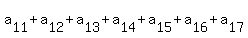 = 44 - 8 = 36. (28)
Next subtract equation (11) from the equation (28). You will get
= 44 - 8 = 36. (28)
Next subtract equation (11) from the equation (28). You will get
 = 36 - 11 = 25. (29)
As the last step, subtract equation (14) from the equation (29). You will get
= 36 - 11 = 25. (29)
As the last step, subtract equation (14) from the equation (29). You will get
 = 25 - 14 = 11. (30)
It is your answer:
= 25 - 14 = 11. (30)
It is your answer:  = 11.
= 11.
Answer.  = 11.
= 11.
* * * S O L V E D * * *