Question 1074455: In 100 persons each man eat 4 fig, woman eat 1 and children eat 1/4 , All of they eat 100 fig, Calculate nos. of man, woman and children among them?
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  = number of men,
 = number of women,
 = number of children
The total is  people, so
 .
The amount of figs eaten is
 .
With the information given we cannot find a unique solution.
The two equations form the system of 2 linear equations on e variables
Your teacher may call the system "dependent," or "underdetermined."
Normally, such a system would give you an infinite N number of solutions.
In this case, because the solutions are numbers of people,
they must be non-negative integers,
so thou will only have many solutions, 21 to be exact.
If you subtract the first equation from the second one,
you get {{100-100=4x+y+0.25z-x-y-z}}}
Multiplying times 4 and dividing by 3
(or you could say multiplying times 4/3),
you get  .
Then, substituting  for in one of the equations,
you can obtain a similar expression
for as a function of :
 .
Your solution is
 .
Giving the values 0, 1, 2, ..., 19, 20 to .
you could calculate and tabulate 21 solutions.
 .
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
In 100 persons each man eat 4 fig, woman eat 1 and children eat 1/4 , All of they eat 100 fig, Calculate nos. of man, woman and children among them?
~~~~~~~~~~~~~~~~~~~~~~~
M + W + C = 100, (1)
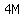 +  +  = 100. (2)
Subtract (1) from (2) (both sides). You will get
3M =  , or M = , or 4M = C.
Thus the number of men must be  times the number of children.
In addition, the number of children must be multiple of 4: 4, 8, 12, 16 . . .
Table
# Children Men M + C Women N-of-figs
1 4 1 5 95 1 + 4*1 + 95 = 100
2 8 2 10 90 2 + 4*2 + 90 = 100
3 12 3 15 85 3 + 4*3 + 85 = 100
4 16 4 20 80 4 + 4*4 + 80 = 100
5 20 5 25 75 5 + 4*5 + 75 = 100
So, any combination C = 4k, M = k, W = 100 - 5k, k = 1, 2, 3, . . . , 20 is the solution.
Check. The number of figs is  = k + 4k + (100-5k) = 100.
Answer. Any combination C = 4k, M = k, W = 100 - 5k, k = 1, 2, 3, . . . , 20 is the solution.
|
|
|
