Question 1071221: How can I solve the equation f(x)=2x^2-8x+2 through factoring?
Found 4 solutions by addingup, josgarithmetic, ikleyn, MathTherapy:
Answer by addingup(3677)   (Show Source):
Answer by josgarithmetic(39617)  (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
1. There is no equation in your post.
2. The fragment "f(x) = 2x^2 -8x + 2" is not an equation.
It is the definition of the function.
3. Since there is no equation in your post, your request makes no sense.
4. Diagnosis: This post doesn't make sense.
-----------------------
comment from student: I am the one who asked about 2x^2-8x+2. I would just like to say that, yes, I am aware
that this is the definition of a function, and I suppose I should have worded my question differently.
I was rather asking how to find the solutions to the function when it is set to equal zero.
Thank you for your 'feedback' but I think you could have been more helpful, or been able to fathom any logical solution
to what I was asking. It isn't that difficult to interpret, and it seems it made sense to two others who decided to help.
-----------------------
My response.
I am really glad to get your comment.
So, I achieved my first goal to convince you that your original formulation was incorrect.
In response, one tutor (josgarithmetic) explained you how to "complete the square".
The other tutor (addingup) showed you how to take the factor "2" out the parentheses.
So, nobody understood your request. Nobody understood what you really want.
It is not amazing.
Yet, we didn't learn to read your thoughts remotely.
We only can read what is written in your post.
Now let's return to your ACTUAL request.
 = 
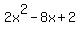The discriminant d = b^2 - 4ac = (-8)^2 - 4*2*2 = 64 - 16 = 48 is not a perfect square of an integer.
So, the equation (and the function) is not factorable in common sense.
The roots ar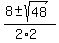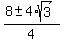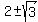e  =  =  =  .
I.e.  =  ,  =  .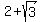
If you want, you can factor the equation (the function) in this way:
f(x) =  =  .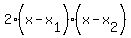
I think, had I not disturb you with my first response, you'd never learned what I wrote to you in this part.
And the best you can do in response is to say "thanks" to me and to learn my lesson.
Answer by MathTherapy(10552)  (Show Source):
|
|
|
