Question 1066754: find the smallest number which is grater than 111,111,000 and divisible by 8 and 9
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE IDEA:
To be divisible by the relatively prime numbers  and and  , ,
a number has to be divisible by 
THE HARD WAY:
Dividing 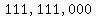 by 72, by 72,
we get 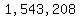 as the quotient, as the quotient,
with  as a remainder, as a remainder,
so 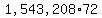 is less than is less than 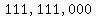 , ,
but the next multiple of  is is
 . .
EASIER:
Dividing 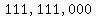 by 72, by 72,
we get 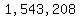 as the quotient, as the quotient,
with  as a remainder, as a remainder,
so adding  to to 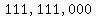
we get the next multiple of  : :
 . .
WITHOUT DIVIDING:
Like all numbers ending in 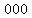 , ,
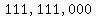 is divisible by is divisible by  , ,
because  is divisible by is divisible by  . .
When dividing by  , ,
the remainder can be found by adding the digits,
and repeating the digit adding with the result,
as many times as needed until you get a single digit result.
The final result is the remainder, unless it is  . .
If the final result is  , ,
then the number is divisible by  , ,
and the remainder is  . .
The sum of the digits of 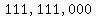 is is  , ,
so when dividing 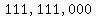 by by  , ,
we get a quotient  , and the remainder is , and the remainder is  . .
So,  is a multiple of is a multiple of  , ,
and it is even a multiple of  , ,
but it is not a multiple of  . .
If I add a multiple of  that is also a multiple of that is also a multiple of  , ,
such as  or or  , ,
the sum will also be a multiple of  and a multiple of and a multiple of  . .
One of those sums must be a multiple of  too. too.
 is not a multiple of is not a multiple of  , ,
because adding digits we get
 and and  , ,
but  is a multiple of is a multiple of  , ,
because  and and  . .
|
|
|