Question 1066667: A factory can produce two products, x and y, with a profit approximated by P =
14x + 24y – 900. The production of y must exceed the production of x by at least 100 units. Moreover, production levels are limited by the formula x + 2y ≤ 1400.
a. Identify the vertices of the feasible region.
b. What production levels yield the maximum profit, and what is the maximum profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your profit equation is p = 14x + 24y - 900
your constraint equations are:
x + 2y <= 1400
y >= x + 100
x >= 0
y >= 0
in the www.desmos.com calculator, you can do the following.
graph the REVERSE inequalities.
if the equation says > you would graph <.
if the equation says >=, you would graph <=.
if the equation says =, you would graph =.
the software will shade the areas of the graph that are NOT in the feasible region.
the region of feasible region will be the areas of the graph that are not shaded.
you could do it directly, but spotting the region of feasibility is easier when you graph the reverse inequalities.
try it yourself.
you will see what i mean.
in fact, i'll show you two graphs.
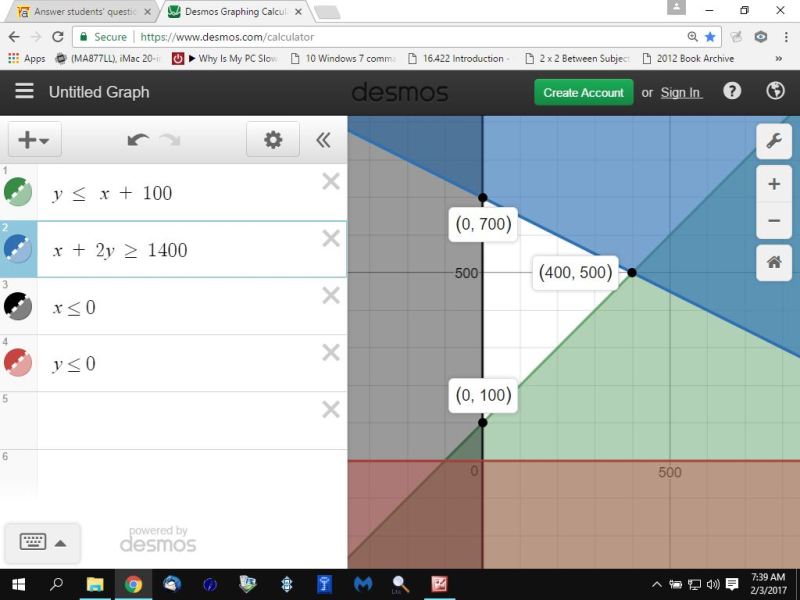
the first graphs the opposite of the region of feasibility.
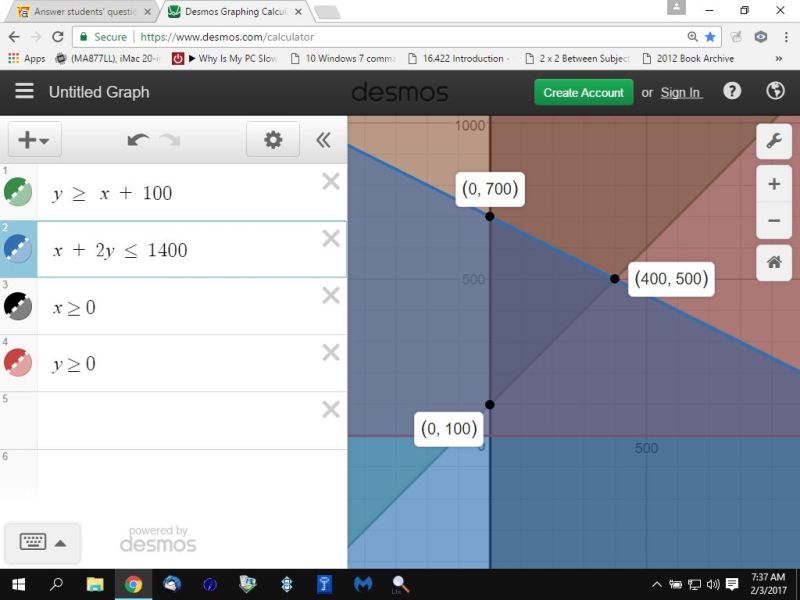
the second graphs the region of feasibility.
in the first graph, you will graph:
x + 2y >= 1400
y <= x + 100
x <= 0
y <= 0
this is opposite of the region of feasibility.
the unshaded area is the region of feasibility.
in the second graph, you will graph:
x + 2y <= 1400
y >= x + 100
x >= 0
y >= 0
the shaded areas is the region of feasibility.
desmos calculator can be found at www.desmos.com/calculator
in both cases, the vertices of the region of feasibility are:
(0,700)
(0,100)
(400,500)
you will analyze the objective function of P = 14x + 24y - 900 at each of the intersection points.
you will get:
(0,700) = 15,900
(0,100) = 1,500
(400,500) = 16,700
your maximum profit is when x = 400 and y = 500
the constraints also have to be satisfied.
y must be greater than x by 100.
since y = 500 and x = 400, this constraint is satisfied.
x + 2y must be smaller than or equal to 1400.
since = 400 and y = 500, then x + 2y = 400 + 1000 = 1400.
this constraint is satisfied also.
the graphs are shown below:
first graph shows inequalities opposite to those required.
second graph shows inequalities directly to those required.
first graph is easier to see the region of feasibility in my opinion.
|
|
|