Question 1045308: a school has fewer than 200 pupils
When they line up on rows of 4 there is 1 extra pupils
When they line up on rows of 5 there is 2 extra pupils
When they line up on rows of 6 there is 3 extra pupils
how many pupils could here be in the school?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = number of pupils in the school. = number of pupils in the school.
When they line up on rows of 4 there is 1 extra pupil left over.
If  more pupils were enrolled, there would be more pupils were enrolled, there would be 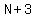 pupils, pupils,
and they could line up in rows of  without any extra pupil left over, because the without any extra pupil left over, because the  new pupils plus the new pupils plus the  pupil previously left over pupil previously left over
would form another row of  pupils. pupils.
So, let's enroll  more pupils, because more pupils, because 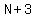 is a multiple of is a multiple of  , ,
and then we can line them all in rows of  without leaving any extra pupils. without leaving any extra pupils.
But what if we want to line them in rows of  ? ?
Well, that works too. We can group the  newly enrolled pupils with the newly enrolled pupils with the  extra pupils that were left over when we only had extra pupils that were left over when we only had  pupils, pupils,
and they could form a new row of  pupils. pupils.
It turns out that 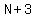 is a multiple of is a multiple of  too. too.
All right, so 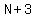 is a good number of pupils if we want to line them up in rows of is a good number of pupils if we want to line them up in rows of  or or  , ,
but what if we want to line them up in rows of  ? ?
It did not work with  pupils, because we had pupils, because we had  extra pupils left over. extra pupils left over.
With those  pupils, and the pupils, and the  newly enrolled pupils, we can make a new row with newly enrolled pupils, we can make a new row with  pupils. pupils.
Wow! It turns out that 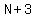 is a multiple of is a multiple of  too. too.
So, 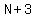 is the right number of pupils for a school that likes to line them up in even rows. is the right number of pupils for a school that likes to line them up in even rows.
That 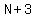 must be a magical number. It is a multiple of must be a magical number. It is a multiple of
 , ,  and and  . .
The least common multiple of  , ,  and and  is is
 , ,
the smaller multiple of  that is also a multiple of that is also a multiple of  , ,  : :
 and and  . .
So, it could be that
 --> -->  ---> --->  , ,
or it could be that
 --> -->  ---> --->  , ,
or it could be that
 --> -->  ---> --->  . .
The next multiple of  , ,  , does not work, , does not work,
because  <---> <--->  makes the number of pupils greater than makes the number of pupils greater than  . .
So the school could have  pupils, or pupils, or  pupils, or pupils, or  pupils. pupils.
|
|
|