SOLUTION: the remainder on division of x^5-x^4+x^3+2x^2-x+4 by x^3+1 is ?

Algebra ->  Equations -> SOLUTION: the remainder on division of x^5-x^4+x^3+2x^2-x+4 by x^3+1 is ?      Log On


   

Question 1044920: the remainder on division of x^5-x^4+x^3+2x^2-x+4 by x^3+1 is ?
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Polynomial division works the same way as regular base-ten division but often is easier. 
             x^2    -x     1
        _______________________________________________
x^3+1   |    x^5   -x^4   x^3    2x^2    -x    4
        |
        |    x^5    0x^4  0x^3   x^2
        -----------------------------
              0    -x^4  x^3    x^2     -x
                   -x^4  0x^3  0x^2    -x
                  ------------------------
                   0     x^3   x^2     0      4
                         x^3   0x^2    0x     1
                        ------------------------
                          0   x^2      0     3


NOTE that the bottom row here shows degree 2, which is less than the degree 3 of the divisor!  Bottom row here represents the REMAINDER.

Remainder is 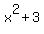x%5E2%2B3, which represents 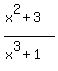%28x%5E2%2B3%29%2F%28x%5E3%2B1%29, just the way you would do if you were dividing plain base-ten numbers.