Question 104461: Here's my questin
Prove a that a root exists for the given function
p(x)=60x(1+x)^72-(1+x)^72+1=0
im assuming you could find the exact value but since they dont ask for the
exact value we would just need to show a solution where p(x)> 0 and where p(x)<0 to prove there is infact a root between the two intervals for ie using the IVT
thanks to any one who can help.
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! 
Let's move some terms around and discuss,
Since 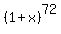 is always positive or zero, let call that A(x) where A(x) is always positive except when x=-1 and A(-1)=0.
Let’s talk about this function for very large positive and negative x.
For even modest values of x (x<-2 and x>0), A(x) grows rapidly because of the power of 72.
For large positive x, A(x) gives a very large, positive number, (60x-1) gives a large, positive number, therefore p(x) is a very large, positive number since positive times a positive equals a positive.
For large negative x, A(x) is a very large, positive number, (60x-1) is a large negative number, therefore p(x) is a very large, negative number since positive times a negative equals a negative.
Therefore between large positive x and large negative x comes a point where p(x)=0, that is, it has a root.
Or using the vocabulary of the IVT,
Since
There exists an x in the interval from  to  where  .
|
|
|
