SOLUTION: "Determine whether each statement is TRUE or FALSE. If FALSE, show or explain how you know." (2k)/(2x+h)=(k)/(x+h) What is the best way to do these problems? To get my answer o

Algebra ->  Equations -> SOLUTION: "Determine whether each statement is TRUE or FALSE. If FALSE, show or explain how you know." (2k)/(2x+h)=(k)/(x+h) What is the best way to do these problems? To get my answer o      Log On


   

Question 1043006: "Determine whether each statement is TRUE or FALSE. If FALSE, show or explain how you know."
(2k)/(2x+h)=(k)/(x+h)
What is the best way to do these problems? To get my answer of false, I plugged in "1" for each variable, is this a valid method?
Found 3 solutions by rothauserc, jim_thompson5910, Edwin McCravy:
Answer by rothauserc(4718) About Me  (Show Source):
You can put this solution on YOUR website!
(2k) / (2x+h) = (k) / (x+h)
:
cross multiply the fractions
:
k(2x+h) = 2k(x+h)
:
2kx + kh = 2kx + 2kh
:
kh = 2kh
:
**********************
The statement is false
**********************
:

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Yes you can plug in any set of values for x, k and h (as long as the denominator isn't zero). So I'm going to plug in x = 0, h = 1 and k = 2.


%282k%29%2F%282x%2Bh%29+=+%28k%29%2F%28x%2Bh%29


%282%2A2%29%2F%282%2A0%2B1%29+=+%282%29%2F%280%2B1%29


%284%29%2F%280%2B1%29+=+%282%29%2F%280%2B1%29


%284%29%2F%281%29+=+%282%29%2F%281%29


4=2 Which is a false equation


So the original equation is false.

Edit: if h = 0 and x was nonzero, then the equation would be true. However, the equation is not true in general. So the answer is still false.

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Well, in this case substituting k = x = h = 1
did happen to work, since
 
%282k%29%2F%282x%2Bh%29=%28k%29%2F%28x%2Bh%29

%282%2A1%29%2F%282%2A1%2B1%29=%281%29%2F%281%2B1%29

2%2F3=1%2F2

which is false.  So k=x=h=1 does produce
a counter-example.

However if the problem had been instead

%282k%29%2F%283x%2Bh%29=%28k%2B4%29%2F%286x%2B4h%29

and you substituted k = x = h = 1 

%282%2A1%29%2F%283%2A1%2B1%29=%281%2B4%29%2F%286%2A1%2B4%2A1%29

2%2F4=5%2F10

1%2F2=1%2F2

That would have been true, not false.  So you would
in that case need to use another number besides 1,
say 2, in order to get a counter-example.

For instance if you substituted k = x = h = 2 in

%282k%29%2F%283x%2Bh%29=%28k%2B4%29%2F%286x%2B4h%29

you get

%284%29%2F%288%29=%286%29%2F%2820%29

1%2F2=3%2F10

which is false.

My point is that you may have to substitute other
values for x, h, and k besides 1 in order to find a 
counter-example.  Never assume that if you get a true 
equation, that the given equation is necessarily true.

In fact in some cases you cannot use the same value
for all the variables.  Take

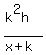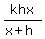%28k%5E2h%29%2F%28x%2Bk%29%22%22=%22%22khx%2F%28x%2Bh%29

If you use the same values for all three variables
you will never get a counter-example.

You'd have to use something like k=1, h=2, and k=3
to get a counter-example.

Edwin