First we get the rectangular equation of the circle.
The center is the polar point, which is
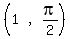 That's the point that we get when we
1. swing counter-clockwise
That's the point that we get when we
1. swing counter-clockwise  radians or 90°
from the right side of the x-axis, and
2. Go out 1 unit in that direction, which
turns out to be directly upward.
So that's the same point as the rectangular point (0,1)
radians or 90°
from the right side of the x-axis, and
2. Go out 1 unit in that direction, which
turns out to be directly upward.
So that's the same point as the rectangular point (0,1)
 So the circle with that center and a radius of
So the circle with that center and a radius of  is this
black circle:
is this
black circle:
 which has rectangular equation:
which has rectangular equation:
 which becomes
which becomes
 or
or



 Then to change from rectangular to polar or
vice-versa we draw this:
Then to change from rectangular to polar or
vice-versa we draw this:
 From which we see that
From which we see that
 ,
,  , and
, and  So we replace the x2+y2 by r2 and
the y using
So we replace the x2+y2 by r2 and
the y using  solved for y,
solved for y,  So the rectangular equation
So the rectangular equation  becomes
the polar equation:
becomes
the polar equation:
 Edwin
Edwin