Question 1039610: 1. x^3 + 64
Factor out. I got (x+4)(x^2-4x+16) but it was wrong.
2. h(x) = x^4 + 4x^3 + 5x^2 + 4x + 4.
Write the polynomial as the product of linear factors?
List all the zeros of the function. (Enter your answers as a comma-separated list.)?
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
You can put this solution on YOUR website! Look at just #1, first.
Can you divide x^3+64 by some binomial factor chosen according to Rational Roots Theorem? You would have x-1, x-2, x-4, x+1, x+2, x+4 to choose from. If you know how to perform synthetic division, then the divisions can be done faster. You would find the right success using the root of -4, or using polynomial division with divisor x+4.
The dividend would be x^3+0x^2+0x+64, and if using or choosing synthetic division, then you would have:
-4 | 1 0 0 64
|
| -4 16 -64
|_____________________________
1 -4 16 0
The remainder is 0, so  is a root. is a root.
The factorization for x^3+0x^2+0x+64 is  , but you were told that this is wrong. , but you were told that this is wrong.
Let us see if that quadratic factor can be factored further. I will try using general solution method for quadratic formula to see if this quadratic has integer roots.
Discriminant is 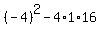
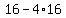

 ----------this discriminant is negative, so this means the roots have Imaginary parts. This means NO Real roots. If you want your factorization of your cubic expression with only showing Real numbers, then this is ----------this discriminant is negative, so this means the roots have Imaginary parts. This means NO Real roots. If you want your factorization of your cubic expression with only showing Real numbers, then this is 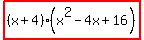 . .
Do you really want the complete factorization including complex factors?
The quadratic factor will have roots
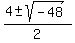
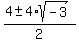
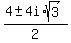
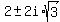
-
Quadratic factor should be 
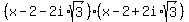
Notice the difference of squares;
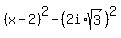
...
but the factorization for the quadratic you want is 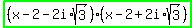 . .
The full factoriztion for x^3+64 is then  . .
|
|
|