Question 1036514: let 
A) calculate f(0), f(1), f(2), f(-1), and f(-2). which of these is useful in factorizing f?
B) from the previous part, you have a factor x - a of f(x) for some a. then you can write 
for some choice of numbers A, B, and C. two of the numbers can be determined by inspection - that is, by looking. which two?
C)by considering the x^2 term (or the x term) on the right hand side, and match with the corresponding piece on the left hand side, compute the remaining number of A, B, and C that you have not yet determined.
D) solve f(x) = 0
E) sketch 
F) use your sketch to solve 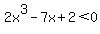
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! A) f(0) = 2, f(1) = -3, f(2) = 4, f(-1) = 7, and f(-2) = 0, all determined by direct substitution.
B)  . .
From part (A), we find that -2 is a zero of f(x), and so x + 2 is a factor of f(x).
==>  . .
Also, it is quite easy to see that A = 2, and the constant C has to be C = 1.
==>  . .
C) Expanding the right-hand side but considering only the coefficient of 0 of  , we get , we get  . .
==> B = -4.
D) Thus  . The other two zeros are . The other two zeros are  . .
E) 
F) This is easy and so I leave this up to you. (Look at the parts of the graph that are below the x-axis.)
|
|
|